 |
| π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 |
Этот неофициальный праздник придумал в 1987 году провозглашенный Принцем Пи сотрудник научно-популярного музея Эксплораториум в Сан-Франциско (San Francisco Exploratorium) физик Ларри Шоу (Larry Shaw), который подметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 — и время 1:59:26 совпадает с первыми разрядами числа π = 3,14159… Обычно празднуют в 1:59 дня (в 12-часовой системе), но придерживающиеся 24-часовой системы считают, что в этот момент время 13:59, и предпочитают отмечать ночью. К слову, в английском языке есть выражение "pi o'clock", означающее время 3:14:15. Впервые День был отмечен в 1988 году в Эксплораториуме. Праздник быстро стал популярным и в 2006 году Конгресс США включил его в официальный список американских праздников, а спустя несколько лет решением ЮНЕСКО за ним закрепили международный статус.
С этим необычным числом мы сталкиваемся уже в младших классах школы, когда начинаем изучать круг и окружность. Число π — математическая константа, выражающая отношение длины окружности к длине ее диаметра. В цифровом выражении π начинается как 3,141592... и имеет бесконечную математическую продолжительность.
 |
| по этим часам всегда час Пи, особенно в 6 часов |
Как считают специалисты, это число было открыто вавилонскими магами. Оно использовалось при строительстве знаменитой Вавилонской башни. Однако, недостаточно точное исчисление (в Древнем Вавилоне его полагали равным 25/8 или 3 1/8) значения π привело к краху всего проекта. Возможно, что эта математическая константа лежала и в основе строительства легендарного Храма царя Соломона.
 |
| Эйнштейн в Волгограде |
 |
| Ларри Шоу, основатель праздника «День пи», в музее Exploratorium |
 |
| так выглядит битва "пирогами" у математиков |
 |
| Пи-рог (Pi Pie) Делфтского университета |
Математик и Козлик
Делили пирог.
Козлик скромно сказал:
- Раздели его вдоль!
- Тривиально! - сказал Математик.-
Позволь,
Я уж лучше
Его разделю поперек! -
Первым он ухватил
Первый кус пирога.
Но не плачьте,
Был тут же наказан порок:
"Пи" досталось ему
(А какой в этом прок?!)
А Козленку...
Козленку достались
Рога!
А еще 3,14 в зеркальном отражении выглядит как слово PIE («пирог», читается «пай», так же как pi). А фраза I prefer pi («я предпочитаю пи») является палиндромом.
 |
| Символ числа Бельфегора |
 |
| Бельфегор. Иллюстрация из книги «Dictionnaire infernal» Колина де Планси, считавшего демона послом ада во Франции |
На худой конец, можно обойтись и пиццей. Кстати, число π поможет вам определиться с выбором пиццы: какую выгоднее заказывать? Казалось бы ответ очевиден: выгоднее, две диаметром 30 см, чем одна диаметром 45 см. Но, на самом деле, все не так просто, как кажется на первый взгляд.
- Для начала посчитаем начинку (иногда начинку пиццы называют топпингом). Казалось бы, начинки больше на двух маленьких. НО! Если взять как данность, что толщина теста 2 см, то площадь бортика двух пицц диаметром 30 см: 2π*[(30/2)2-(26/2)2]=351.8583772 см2. А значит, полезная площадь, т.е. та, на которой лежит начинка: 1061.858317 см2. Теперь разберемся с 45 см. Общая площадь её бортиков: π*[(45/2)2-(41/2)2]=270.1769682 см2, соответственно полезная - 1320.254313 см2. Взяв соотношение площадей пицц, получим: 1320.254313/1061.858317=1.243343195. Т.е. начинки на двух маленьких пиццах почти на четверть меньше, чем на одной большой.
- А что если за точку отсчета (или, вернее, рассчета) взять не количество начинки, а вес? Вес 30 сантиметровой пиццы примерно 750 грамм, в то время как одна большая весит 1-1.2 килограмма. Но, ведь почти 30% от веса пиццы – это тесто по бортам пиццы. Тогда получается, что одна большая – выгоднее, чем 2 маленькие.
- А как быть с диаметром? Может, здесь две маленькие больше, чем одна большая? Площадь круга никто не забыл? πr2 (если что). Тогда вперед, за истиной. Площадь двух пицц по 30 см: 2π*(30/2)2=1413 см2. Площадь одной пиццы 45 см: π*(30/2)2=1590 см2. И опять одна, но большая, лучше, чем две маленькие…
Студенты же и школьники в этот день проводят флешмобы:
В 2001 необычно отметили день π шестиклассники одной из средних школ Хакеттстауна, выстроившись в школьном дворе в форме греческой буквы π, у каждого в руках была карточка с цифрой из этого числа.
14 февраля 2013, в рамках III Фестиваля науки, прошедшего в Ульяновске, студенты ульяновских вузов провели акцию "Я люблю науку!" установили рекорд — они выстроились на эспланаде от площади имени 100-летия со дня рождения Ленина до площади Ленина в цепочку, держа в руках таблички с цифрами числа π, воссоздав знаменитое число до 434-й цифры после запятой (табличка с запятой досталась одному из организаторов акции, начальнику отдела координации научной деятельности правительства Ульяновской области Дмитрию Серенко). По словам организаторов, это самый большой результат подобных акций в России, который будет занесен в Книгу рекордов России.
Христиан Крюзер, давний любитель числа π, не только взял это число с собой в полет (фото слева), но и заставил его (наверняка не спросив) совершить прыжок вместе с группой парашютистов. Он же установил памятный знак π (фото справа) на одной из высочайших вершин мира - пик Ленина.
12 сентября 2012 года 1000 гигантских знаков после запятой числа π появились в небе над Сан-Франциско и окрестностями. Эту акцию затеял художник, известный как ISHKY, вместе с фирмой Stamen Design, а весь проект назывался "Pi in the Sky" (кстати, если поделить окружность Солнца на его диаметр получится «Журавль в небе» (идиома pi in the sky, означающая нечто недоступное)). 5 самолётов облетели залив Сан-Франциско, сделав круг размером 160 км, и «написали» в небе число π, распыляя «пиксели» с помощью специально запрограммированной системы.
Математики нашли новое число - "Во", они прибавляют его к числу "Пи" и очень довольны
Также в этот день необходимо пить напитки, начинающиеся на «пи». Правда, на поверку таких напитков оказывается не так уж и много, разве что пи-во. Еще в нэте удалось найти экзотический пенный напиток «Пи-цзю». Впрочем, пи-цзю – это то же пи-во, только китайское (а "цзю" - это любой алкоголь вообще)...
 |
| Произношение: pi jeou кстати, вы заметили в иероглифе цзю букву π? |
 |
| Кстати, 45º = π/4 |
Анекдот по теме
Двое студентов времён СССР, второкурсник и первокурсник, ведут диалог о крепких спиртных напитках.
1-й: 2,12 — это что такое?
2-й: "Перцовка".
1-й: А 2,62?
2-й: «Кубанская», конечно.
1-й: Ну, 2,87, это ты и так знаешь…
2-й: Ясное дело: «Московская особая».
1-й: 3.07?
2-й: «Столичная».
1-й: 3,12?
2-й: «Старка».
1-й: 3,14?
2-й (мучительно соображает, потом неуверенно): Может, какая-нибудь импортная?
1-й (торжествующе): Дурак ты! Это число «Пи». А еще математик…
Баллада об Учёном Чёрном Колпаке и Числе Пи
"- Милорд, не печалься, бывает и так,
Что умным в беде помогает дурак."
С.Я. Маршак. "Король и Пастух"
В городе Икс, за горами, морями
Жил математик с тремя сыновьями.
Старший - любил математику очень.
Средний - любил ее так, между прочим.
Младший был мало похож на папашу -
Водку любил и буфетчицу Глашу.
Как-то, наследством своим озабочен,
Вызвал отец сыновей среди ночи.
Выдал Хрущевской эпохи монеты
И приказал: "До начала рассвета
Нужно без циркуля и без линейки
Вычислить Пи для рубля и копейки.
Тот, чье решенье окажется краше,
В жены получит буфетчицу Глашу,
Черный колпак и сто грамм на похмелье",-
Так он сказал, и ушел в свою келью.
Время пошло, и в раздумьи над кодом
Каждый своим отличился подходом.
Старший задание счел несуразным:
"Пи не бывает для разного разным."
Средний был в том не уверен, но все-же
Быстро смекнул, что перечить дороже.
Младший задул догоравшую свечку,
Выпил, икнул и вернулся на печку.
Думая час, и не видя просвета,
Старшие братья пошли за советом.
Всех обошли этой ночью бессонной:
Были у Крулеров, у Бенинсонов.
Стыдно сказать, даже сам Ломоносов
Не избежал полуночных распросов.
Еле успели домой до рассвета,
Где их отец дожидался с ответом.
Старший вздохнул и сказал виновато:
"Ночи на брата, отец, маловато".
Средний добавил, косясь под скамейку:
"Кабы нам циркуль, да кабы линейку..."
Младший сын вышел нетвердой походкой:
"Помню я старые цены* на водку.
Если налить пол-литровую кружку,
И возвести в ее степень чекушку,
То по тем ценам выходит, однако,
В точности Пи, вплоть до третьего знака".
Встал тут отец, преподнес ему чашу,
Черный колпак и буфетчицу Глашу.
Долго не думая, свадьбу сыграли...
Мы же добрались до главной морали:
Чтоб получить чье-то сердце и руку,
Нужно учить прикладную науку.
Александр Гурарий
*** из письма, отправленного Питером Умновым из палаты «Дома Тихого Отдыха» на Пряжке - в редакцию журналов «Оракул» и «Час Пик» перед Днём числа Пи - 14 марта:
«…Не обращал вниманья на наружность,
И хоть все в Доме убеждают: - « Не глупи!..»,
Упорно на диаметр делю окружность,
Но всякий раз в итоге получаю: ПИ!!!
Уже дошёл до миллионных знаков,
Считая после трёх и после запятой,
А ПИ – всё не кончается, собака!
Я заПИл резко: ПИлотировал в запой!..
ПИсака ПИво ПИл, ЧИСЛО - ПИарил -
Закусывал чем? К ПИву ПИщу - ПИроги…
Знак «ПИ» Вселенную как шифр затоварил:
В мозгу – лишь ПИ! ПИжон! И ПИкнуть – не могИ!
В ПИ зашифрован первобытный хаос,
ПИлюля мистики, для всех ПИ - ПИетизм...
ПИла, ПИгмей, ПИсатель – всё сломалось:
ПИИТ, ПИр духа, каПИтал-консерватизм!
Как ПИфия при храме восседаю,
Чтоб разделить окружность на сверх-цифру ПИ...
Диаметр – вещь, знаю: вовсе не простая…
В ДЕНЬ ПИ – даёшь ДЕНЬ ВЫХОДНОЙ! Чего глуПИть?
Любимый город? Безусловно ПИтер!
ПИшу поэму «ПИфагоровы штаны»,
Мой стих, - предприниматели, – куПИте!
ПИсьмо - о роли цифры ПИ - для всей страны!
…Бросаю ПИть! Мой слог – стопа – ПИррихий!!
В ПИ раз зарплату увеличьте, снизив боль!
Защиты от ПИявок нет…Я ж – тихий…
А для защиты выдайте большой ПИстОль!..
…Психологи вживляют в душу нити:
Я миллионы знаков вычислить готов!
В «Оракуле», в «ЧАС ПИК» - мой «НИК» смените!
В Союз ПИ-сателей факс:
…..ПОДПИСЬ: П.И.Умнов!»
……………………………………………….
…И я дошёл до миллионных знаков,
Считая после трёх и после запятой,
А ПИ – всё не кончается, собака!
…Когда бороться с водкой? - Не уйти в запой!..
* - нич /лич, Питер Иванович Умнов – известный (узкому кругу ограниченных лиц) математик
** - рисуночек «ПИ до миллионного знака» - свой
*** - все совпадения случайны, все несовпадения - тоже
Валерий Таиров
Жизнь без Пи представить невозможно.
..во без Пи, как без ружья боец.
Вкус без Пи совсем не тот у ..рожных
И у ..зды без пи полнейший ..здец.
Finist
Что ж, наконец добрались и до истины,
А истина, естественно - конец...
Лес не бывает (даже с ПИ) безлиственный,
Без ПИ - действительно, невкусный х..олодец!
Валерий Таиров
ПИит ПИсал в ПИжаме много знаков,
Как Пионер, сорвавшийся с цеПИ,
Но ручку расПИсать не смог однако,
В ПИанке не набрал в неё чернил……
Станислав Абрамов
Чернила ПИть нельзя - беречь их надо,
Чтоб перья на ПИсульках не туПИть...
А если про ПИкеты и ПАрады -
Заправлю ручку сладким шоколадом,
Сигналя словно спутник: Пи-пи-Пи...
Валерий Таиров
 |
| с такими π-ледышками, любой коктейль, станет π-коктейлем |
Для визуального же ликбеза рекомендуется просмотр дебютного фильма небезызвестного режиссера Даррена Аронофски «Пи» (1998 г., США, сюрреалистический психологический триллер, с бюджетом в $60000, собравший в прокате $3,2 млн, что позволило расплатиться с долгами и планировать свою следующую работу). Главный герой фильма — талантливый математик Макс Коэн, живущий один в своей комнате, больше похожей на огромный единый механизм, в течение многих лет пытается найти и расшифровать универсальный цифровой код, согласно которому изменяются курсы всех биржевых акций. Он изобретает компьютер «Евклид» («Эвклид»), который однажды выдаёт ему некое 216-значное число, которое может отражать присутствие Бога в этом мире. (Кстати, длинный набор цифр, появляющихся в начале фильма, репрезентирует число π только до девятого знака после запятой — дальше идёт просто набор цифр.) По мере приближения к разгадке, мир вокруг Макса превращается в мрачный кошмар: его преследуют могущественные аналитики с Уолл-стрит и религиозные фанатики, готовые пойти на убийство, чтобы обнаружить код вселенского мироздания в своих древних священных текстах. Находясь на грани безумия, Макс должен сделать решающий выбор между порядком и хаосом, святостью и дьявольщиной, мудростью и невежеством, и решить, способен ли он совладать с могущественной силой, которую пробудил его гениальный разум.
А это музончик из того же фильма: "2πr" Clint Mansell. Как раз для середины дня...
 |  |
| схема из книги Oedipus Aegyptiacus (1652—1654) Афанасия Кирхера | "упоминание" π в имени тетраграмматона |
- В древнееврейской системе чисел нет нуля;
- Древнееврейская система чисел является непозиционной;
- Большинство иудейских букв соответствуют двух- или трехзначным цифрам.
В американском ситкоме Чака Лорри и Билла Прэди "Теория большого взрыва" о жизни двух молодых талантливых физиков (Шелдон Купер и Леонард Хофстедтер) и их привлекательной соседке по лестничной площадке: номер квартиры, в которой живет Эми – 314 – это число π.
π служит секретным кодом в американском шпионском фильме Альфреда Хичкока «Разорванный занавес» (1966) и американском же триллере на тему высоких технологий «Сеть» (1995) с восходящей на тот момент звездой Сандрой Буллок (играет специалистку по бета-тестированию Анджелу Беннет, получившую от своего коллеги Дейла, погибшего вскоре в странной авиакатастрофе, вызванной сбоем электронной системы навигации, экземпляр троянской программы, внедряемой преступной группировкой кибертеррористов под видом охранной программы в важные компьютерные системы — в банки, аэропорты и даже базы данных ФБР...).
Российский производитель Nexters порадовал игроков браузеркой в жанре комиксов и ужасов, привлекающей к себе внимание не только монстрами и чудищами, но и интеллектуальными квестами, приправленными «ядерным» черным юмором. "...В Россию завезли Большой Адронный Коллайдер. Направляясь к пункту назначения доставки, в Коллайдер врезался автомобиль. Произошла утечка химического вещества, которая привела к полному уничтожению всего живого и с этого начинается игра с соответствующим названием - Полный Пи". Говорят, что эта бесплатная ролевая онлайн игра действительно разрывает все шаблоны игр своего жанра.
А вот фильм
рекомендуется к просмотру только после изрядной дозы π-ва, когда вам будет уже настолько хорошо, что лень будет думать о жизни, Вселенной и прочей ерунде. Потому как и Сам (Пелевин) предостерегает: «Не ищи во всем символического значения, а то ведь найдешь... На свою голову».
К тому же в романе "Мастер и Маргарита" события главы "Понтий Пилат" происходят в день числа "Пи" - 3,1416. 14 ниссана, 14 - 16 марта. Они же мартовские Иды (берегись мартовских Ид). В этой главе Пилат (прошу обратить внимание на начало "Пи" в его имени) в Зените славы (Солнце прямо над ним) смотрит на Солнце и слепнет. У него ужасно болит голова. Именно об этом рассказывает и главный герой в самом начале фильма "Пи" Даррена Аронофски.
 |
| Скатерть Улама |
Получается, что это число (единственное разумное число во Вселенной!) и управляет нашим миром.
Более того - учёные установили, что именно через π можно определить местоположение элементарных частиц в Таблице элементарных частиц (ранее это пытались сделать через Таблицу Вуди), а сообщение о том, что в недавно расшифрованном ДНК человека число π отвечает за саму структуру ДНК (достаточно сложную, надо отметить), произвело эффект разорвавшейся бомбы! ак считает доктор Чарльз Кэнтор, под руководством которого ДНК и было расшифровано: "Такое впечатление, что мы подошли к разгадке некоей фундаментальной задачки, которую нам подкинуло мироздание. Число π - повсюду, оно контролирует все известные нам процессы, оставаясь при этом неизменным! Кто же контролирует само число Пи? Ответа пока нет". а самом деле, Кэнтор лукавит, ответ есть, просто он настолько невероятен, что учёные предпочитают не выносить его на широкую публику, опасаясь за собственную жизнь (об этом чуть позже): число π само себя контролирует, оно разумно! Вздор? Не спешите. Ведь ещё Фонвизин говорил, что "в человеческом невежестве весьма утешительно считать всё то за вздор, чего не знаешь".
Во-первых, догадки о разумности чисел вообще давно посещали многих известных математиков современности. Норвежский математик Нильс Хенрик Абель в феврале 1829-го писал своей матери: "Я получил подтверждения того, что одно из чисел - разумно. Я говорил с ним! Но меня пугает, что я не могу определить, что это за число. Но может быть это и к лучшему. Число предупредило меня, что я буду наказан, если Оно будет раскрыто". Кто знает, раскрыл бы Нильс значение числа, с ним говорившего, но 6 марта 1829-го года его не стало.
1955 год, японец Ютака Танияма выдвигает гипотезу о том, что "каждой эллиптической кривой соответствует определенная модулярная форма" (как известно, на основе этой гипотезы была доказана теорема Ферма). 15 сентября 1955-го, на международном математическом симпозиуме в Токио, где Танияма объявил о своей гипотезе, на вопрос журналиста: "Как вы до этого додумались?" - Танияма отвечает: "Я не додумался, число мне об этом сообщило по телефону". Журналист, думая, что это шутка, решил её "поддержать": "А номер-то телефона оно вам сообщило?". На что Танияма серьёзно ответил: "Такое впечатление, что этот номер мне давно был известен, но я могу теперь сообщить его только через 3 года, 51 день, 15 часов и 30 минут." В ноябре 1958 года Танияма покончил с собой. 3 года, 51 день, 15 часов и 30 минут - это и есть 3,1415. Совпадение? Может быть. Но - вот ещё одно, ещё более странное. Итальянский математик Селла Квитино тоже несколько лет, как он сам туманно выражался, "поддерживал связь с одной милой цифрой". Цифра, по словам Квитино, который уже тогда лежал в психиатрической лечебнице, "обещала сказать своё имя в день своего рождения". Мог ли Квитино настолько лишиться разума, чтобы называть число π цифрой, или он так специально запутывал врачей? Не ясно, но 14 марта 1827-го года Квитино не стало.
А самая загадочная история связана с "великим Харди" (как вы все знаете, так современники называли великого английского математика Годфри Харолда Харди, члена Лондонского королевского общества (1910), иностранного член-корреспондента (1924) и почётного члена АН СССР (1934), иностранного члена Национальной академии наук США (1927), Французской академии наук (1947; корреспондент с 1945)), который вместе со своим приятелем Джоном Литлвудом знаменит работами в теории чисел (особенно в области диофантовых приближений) и теории функций (где друзья прославились исследованием неравенств). В дополнение к его исследованиям, его помнят за его эссе 1940 года об эстетике математики под названием «Апология математика», в которос кроме всего прочего прокомментировал фразу, приписываемую Карлу Фридриху Гауссу: «Математика — царица наук, а теория чисел — королева математики», означавшее, по мнению Харди, что основные понятия, составляющие теорию чисел, глубже и элегантнее по сравнению с любой другой областью математики. Как известно, Харди был официально неженат, хотя не раз заявлял, что "обручён с царицей мира нашего". Коллеги-учёные не раз слышали, как он разговаривает с кем-то в своём кабинете, его собеседника никто никогда не видел, хотя его голос - металлический и чуть скрипучий - долгое время был притчей во языцех в Оксфордском университете, где он работал в последние годы. В ноябре 1947 года эти беседы прекращаются, а 1 декабря 1947 года Харди находят на городской свалке, с пулей в желудке. Версию о самоубийстве подтвердила и записка, где рукой Харди было написано: "Джон, ты увёл у меня царицу, я тебя не виню, но жить без неё я более не могу".
Связана ли эта история с числом Пи? Пока неясно, но не правда ли, любопытно?
Вообще говоря, подобных историй можно накопать очень много, и, разумеется, не все они трагичны.
| Формула Бэйли-Боруэйна-Плаффа (BBP-формула, Формула ББП) для вычисления n-го знака числа π в шестнадцатеричной системе счисления |
Ричард Грендел из колледжа Reed College в Портланде, США, рассматривая число с другой стороны, т.е. пытаясь найти какой-то смысл и порядок в кажущемся хаотичном ряду цифр после запятой, установил, что регулярно повторяюющуюся комбинации цифр 59345 и 78952. Впрочем, вопрос о том, является ли повторение случайным или закономерным, пока остается открытым. Между тем, открытие прокладывает путь к разгадке числа π и в целом к определению его сути — является ли оно нормальным для нашего мира или нет. Математик интересуется числом π с 1996 года, и с этого времени ему пришлось отказаться от так называемой «теории чисел» и обратить внимание на «теорию хаоса», являющуюся ныне его главным оружием.
Даниэль А. Беккер — выпускник университета прикладной науки Mainz, задался вопросом "Как выглядит случайность?" В случае с числом π по выборке в 1 миллион десятичных разрядов Даниэль сделал следующие наблюдения. Число π имеет бесконечное число знаков после запятой, неопознаваемые системы последовательности. Однако, распределение из 10 возможных цифр довольно равномерно сбалансированно — по крайней мере в диапазоне от 1 до 1000000 позиций после запятой. Каждая цифра представляет собой направление от 0° до 360°. Например, каждый раз, когда возникает 0, линия с определенной фиксированной длиной отображаются со значением 0°. В конце каждой линии в то же самое время начинается линия для следующей цифры; длина каждой линии остается постоянной. Результатом этих линий является путь, так называемые блуждания /произвольное движение. Цветные районы представляют распределение десятичных разрядов π. Они всегда начинаются с 0, но при каждом последующем шаге значения увеличиливаются на 10000. Эти области лежат вокруг наиболее крайних точек блуждания. Как можно заметить, чем больше становится отображаемый диапазон, тем круглее эти области.
Порядок: чем больше диапазон наблюдаемых десятичных разрядов, тем более сбалансированно распределение цифр от 0 до 9.
Хаос: распределение, частота и последовательность десятичных разрядов числа π не поддается систематизации.
Собственно, эту картинку, которую можно сравнить и с мозгом, и со звёздной туманностью, можно смело называть "мозгом числа Пи". Примерно с помощью такой структуры это число (единственное разумное число во вселенной) и управляет нашим миром. Но - каким образом происходит это управление? Как правило, с помощью неписанных законов физики, химии, физиологии, астрономии, которые контролируются и корректируются разумным числом. Приведённые выше примеры показывают, что разумное число так же нарочно персонифицируется, общаясь с учёными как некая сверхличность. Но если так, приходило ли число π в наш мир, в облике обычного человека?
Сложный вопрос. Может быть приходило, может быть нет, надёжной методки определения этого нет и быть не может, но, если это число во всех случаях определено само собой, то можно предположить, что оно приходило в наш мир как персона в день, соответствующий его значению. Разумеется, идеальной датой рождения π является 14 марта 1592-го года (3,141592), однако, надёжной статистики по этому году, увы, нет - известно только, что именно в том году 14 марта родился фаворит и первый министр королей Якова I и Карла I Стюартов Джордж Вильерс Бэкингем - герцог Бэкингем из "Трёх мушкетёров" Александра Дюма. Он великолепно фехтовал, знал толк в лошадях и соколиной охоте - но был ли он числом π? Вряд ли. На роль человеческого воплощения числа π мог бы идеально претендовать Дункан МакЛауд, родившийся 14-го марта 1592-го года, в горах Шотландии - если бы был реальной личностью. Но ведь год (1592) может определяться по собственному, более логичному для π летоисчислению. Если принять это предположение, то претендентов на роль числа π становится много больше.
Самый очевидный из них — Альберт Эйнштейн, родившийся 14 марта 1879-го*. Но 1879 год это и есть 1592 год относительно 287 года до нашей эры! А почему именно 287? Да потому что именно в этом году родился Архимед, впервые в мире вычисливший число π как отношение длины окружности к диаметру и доказавший, что оно одинаково для любого круга! Совпадение? Но не много ли совпадений, как думаете?
* День π — это также день рождения:
- австрийского композитора, скрипача, дирижёра Иоганна Батиста Штрауса (1804), более известного как Иоганн Штраус-отец, написавшего множество музыкальных произведений, в том числе и знаменитейший Марш Радецкого;
- итальянского астронома Джованни Вирджинио Скиапарелли (1835), наблюдавшего на поверхности Марса (во время великого противостояния 1877 г.) прямые линии, названые им — «canali» (с итальянского обозначает протоки естественного или искусственного происхождения, и может переводиться на английский как «grooves», «channels» или «canals» (последнее слово, употребляющееся для каналов искусственного происхождения, использовавшееся при переводе его работ и послужило в конце XIX — начале XX века распространению точка зрения об искусственном происхождении «каналов» и существовании на Марсе цивилизации);
- Элджернона Генри Блэквуда (1869), английского искателя приключений и писателя, опубликовавшего немало историй о необычном и сверхъестественном, а в последние годы жизни часто выступавшего на радио и телевидении, читая легенды о призраках и привидениях;
- последнего человека, побывавшего на Луне, Юджина Эндрю «Джина» Сернана (1934), американского астронавта чехо-словацкого происхождения: "Сегодняшний вызов Америки определил будущие судьбы человечества. И, покидая Луну в [районе] Таурус-Литтров, мы уходим так же как и пришли и, с Божьей помощью, вернёмся — с миром и надеждой для всего человечества";
- небезызвестного стендапера и агента Comedy Club, безграмотного экс-учителя русского языка и литературы, экс-капитана пензенской команды КВН «Валеон Дассон» и экс-диджея «Русского радио в Пензе», озвучивавшего Масяню в шоу "В гостях у Масяни" на "Муз-ТВ", гламурного подонка Павла «Снежка» Воли (1979).
В какой личности π персонифицировано сегодня, не ясно [кстати, 14 марта 1988 родилась самая знаменитая американская порноактриса (бывшая), известная также своим творчеством в сфере кинематографа, моды и музыки (бывшая участница музыкальной группы aTelecine, играющей электро-индастриал) — Саша Грей (настоящее имя Марина Энн Хэнцис)], но для того, что бы увидеть значение этого числа для нашего мира, не нужно быть математиком: π проявляется во всём, что нас окружает. И это, кстати, очень свойственно для любого разумного существа, каковым, без сомнения, является π!
Неуловимый Джа (xa__)
Кстати, поскольку в нашем мире существует такое красивое число, как Пи, которое бесконечно и нет правила хранить все это в конечном объеме памяти, наша Вселенная должна быть реальной. Эта философская формулировка, является контраргументом аргументу, что наша Вселенная может быть компьютерной симуляцией.
3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9848824012 8583616035 6370766010 4710181942 9555961989 4676783744 9448255379 7747268471 0404753464 6208046684 2590694912 9331367702 8989152104 7521620569 6602405803 8150193511 2533824300 3558764024 7496473263 9141992726 0426992279 6782354781 6360093417 2164121992 4586315030 2861829745 5570674983 8505494588 5869269956 9092721079 7509302955 3211653449 8720275596 0236480665 4991198818 3479775356 6369807426 5425278625 5181841757 4672890977 7727938000 8164706001 6145249192 1732172147 7235014144 1973568548 1613611573 5255213347 5741849468 4385233239 0739414333 4547762416 8625189835 6948556209 9219222184 2725502542 5688767179 0494601653 4668049886 2723279178 6085784383 8279679766 8145410095 3883786360 9506800642 2512520511 7392984896 0841284886 2694560424 1965285022 2106611863 0674427862 2039194945 0471237137 8696095636 4371917287 4677646575 7396241389 0865832645 9958133904 7802759009 9465764078 9512694683 9835259570 9825822620 5224894077 2671947826 8482601476 9909026401 3639443745 5305068203 4962524517 4939965143 1429809190 6592509372 2169646151 5709858387 4105978859 5977297549 8930161753 9284681382 6868386894 2774155991 8559252459 5395943104 9972524680 8459872736 4469584865 3836736222 6260991246 0805124388 4390451244 1365497627 8079771569 1435997700 1296160894 4169486855 5848406353 4220722258 2848864815 8456028506 0168427394 5226746767 8895252138 5225499546 6672782398 6456596116 3548862305 7745649803 5593634568 1743241125 1507606947 9451096596 0940252288 7971089314 5669136867 2287489405 6010150330 8617928680 9208747609 1782493858 9009714909 6759852613 6554978189 3129784821 6829989487 2265880485 7564014270 4775551323 7964145152 3746234364 5428584447 9526586782 1051141354 7357395231 1342716610 2135969536 2314429524 8493718711 0145765403 5902799344 0374200731 0578539062 1983874478 0847848968 3321445713 8687519435 0643021845 3191048481 0053706146 8067491927 8191197939 9520614196 6342875444 0643745123 7181921799 9839101591 9561814675 1426912397 4894090718 6494231961 5679452080 9514655022 5231603881 9301420937 6213785595 6638937787 0830390697 9207734672 2182562599 6615014215 0306803844 7734549202 6054146659 2520149744 2850732518 6660021324 3408819071 0486331734 6496514539 0579626856 1005508106 6587969981 6357473638 4052571459 1028970641 4011097120 6280439039 7595156771 5770042033 7869936007 2305587631 7635942187 3125147120 5329281918 2618612586 7321579198 4148488291 6447060957 5270695722 0917567116 7229109816 9091528017 3506712748 5832228718 3520935396 5725121083 5791513698 8209144421 0067510334 6711031412 6711136990 8658516398 3150197016 5151168517 1437657618 3515565088 4909989859 9823873455 2833163550 7647918535 8932261854 8963213293 3089857064 2046752590 7091548141 6549859461 6371802709 8199430992 4488957571 2828905923 2332609729 9712084433 5732654893 8239119325 9746366730 5836041428 1388303203 8249037589 8524374417 0291327656 1809377344 4030707469 2112019130 2033038019 7621101100 4492932151 6084244485 9637669838 9522868478 3123552658 2131449576 8572624334 4189303968 6426243410 7732269780 2807318915 4411010446 8232527162 0105265227 2111660396 6655730925 4711055785 3763466820 6531098965 2691862056 4769312570 5863566201 8558100729 3606598764 8611791045 3348850346 1136576867 5324944166 8039626579 7877185560 8455296541 2665408530 6143444318 5867697514 5661406800 7002378776 5913440171 2749470420 5622305389 9456131407 1127000407 8547332699 3908145466 4645880797 2708266830 6343285878 5698305235 8089330657 5740679545 7163775254 2021149557 6158140025 0126228594 1302164715 5097925923 0990796547 3761255176 5675135751 7829666454 7791745011 2996148903 0463994713 2962107340 4375189573 5961458901 9389713111 7904297828 5647503203 1986915140 2870808599 0480109412 1472213179 4764777262 2414254854 5403321571 8530614228 8137585043 0633217518 2979866223 7172159160 7716692547 4873898665 4949450114 6540628433 6639379003 9769265672 1463853067 3609657120 9180763832 7166416274 8888007869 2560290228 4721040317 2118608204 1900042296 6171196377 9213375751 1495950156 6049631862 9472654736 4252308177 0367515906 7350235072 8354056704 0386743513 6222247715 8915049530 9844489333 0963408780 7693259939 7805419341 4473774418 4263129860 8099888687 4132604721 5695162396 5864573021 6315981931 9516735381 2974167729 4786724229 2465436680 0980676928 2382806899 6400482435 4037014163 1496589794 0924323789 6907069779 4223625082 2168895738 3798623001 5937764716 5122893578 6015881617 5578297352 3344604281 5126272037 3431465319 7777416031 9906655418 7639792933 4419521541 3418994854 4473456738 3162499341 9131814809 2777710386 3877343177 2075456545 3220777092 1201905166 0962804909 2636019759 8828161332 3166636528 6193266863 3606273567 6303544776 2803504507 7723554710 5859548702 7908143562 4014517180 6246436267 9456127531 8134078330 3362542327 8394497538 2437205835 3114771199 2606381334 6776879695 9703098339 1307710987 0408591337 4641442822 7726346594 7047458784 7787201927 7152807317 6790770715 7213444730 6057007334 9243693113 8350493163 1284042512 1925651798 0694113528 0131470130 4781643788 5185290928 5452011658 3934196562 1349143415 9562586586 5570552690 4965209858 0338507224 2648293972 8584783163 0577775606 8887644624 8246857926 0395352773 4803048029 0058760758 2510474709 1643961362 6760449256 2742042083 2085661190 6254543372 1315359584 5068772460 2901618766 7952406163 4252257719 5429162991 9306455377 9914037340 4328752628 8896399587 9475729174 6426357455 2540790914 5135711136 9410911939 3251910760 2082520261 8798531887 7058429725 9167781314 9699009019 2116971737 2784768472 6860849003 3770242429 1651300500 5168323364 3503895170 2989392233 4517220138 1280696501 1784408745 1960121228 5993716231 3017114448 4640903890 6449544400 6198690754 8516026327 5052983491 8740786680 8818338510 2283345085 0486082503 9302133219 7155184306 3545500766 8282949304 1377655279 3975175461 3953984683 3936383047 4611996653 8581538420 5685338621 8672523340 2830871123 2827892125 0771262946 3229563989 8989358211 6745627010 2183564622 0134967151 8819097303 8119800497 3407239610 3685406643 1939509790 1906996395 5245300545 0580685501 9567302292 1913933918 5680344903 9820595510 0226353536 1920419947 4553859381 0234395544 9597783779 0237421617 2711172364 3435439478 2218185286 2408514006 6604433258 8856986705 4315470696 5747458550 3323233421 0730154594 0516553790 6866273337 9958511562 5784322988 2737231989 8757141595 7811196358 3300594087 3068121602 8764962867 4460477464 9159950549 7374256269 0104903778 1986835938 1465741268 0492564879 8556145372 3478673303 9046883834 3634655379 4986419270 5638729317 4872332083 7601123029 9113679386 2708943879 9362016295 1541337142 4892830722 0126901475 4668476535 7616477379 4675200490 7571555278 1965362132 3926406160 1363581559 0742202020 3187277605 2772190055 6148425551 8792530343 5139844253 2234157623 3610642506 3904975008 6562710953 5919465897 5141310348 2276930624 7435363256 9160781547 8181152843 6679570611 0861533150 4452127473 9245449454 2368288606 1340841486 3776700961 2071512491 4043027253 8607648236 3414334623 5189757664 5216413767 9690314950 1910857598 4423919862 9164219399 4907236234 6468441173 9403265918 4044378051 3338945257 4239950829 6591228508 5558215725 0310712570 1266830240 2929525220 1187267675 6220415420 5161841634 8475651699 9811614101 0029960783 8690929160 3028840026 9104140792 8862150784 2451670908 7000699282 1206604183 7180653556 7252532567 5328612910 4248776182 5829765157 9598470356 2226293486 0034158722 9805349896 5022629174 8788202734 2092222453 3985626476 6914905562 8425039127 5771028402 7998066365 8254889264 8802545661 0172967026 6407655904 2909945681 5065265305 3718294127 0336931378 5178609040 7086671149 6558343434 7693385781 7113864558 7367812301 4587687126 6034891390 9562009939 3610310291 6161528813 8437909904 2317473363 9480457593 1493140529 7634757481 1935670911 0137751721 0080315590 2485309066 9203767192 2033229094 3346768514 2214477379 3937517034 4366199104 0337511173 5471918550 4644902636 5512816228 8244625759 1633303910 7225383742 1821408835 0865739177 1509682887 4782656995 9957449066 1758344137 5223970968 3408005355 9849175417 3818839994 4697486762 6551658276 5848358845 3142775687 9002909517 0283529716 3445621296 4043523117 6006651012 4120065975 5851276178 5838292041 9748442360 8007193045 7618932349 2292796501 9875187212 7267507981 2554709589 0455635792 1221033346 6974992356 3025494780 2490114195 2123828153 0911407907 3860251522 7429958180 7247162591 6685451333 1239480494 7079119153 2673430282 4418604142 6363954800 0448002670 4962482017 9289647669 7583183271 3142517029 6923488962 7668440323 2609275249 6035799646 9256504936 8183609003 2380929345 9588970695 3653494060 3402166544 3755890045 6328822505 4525564056 4482465151 8754711962 1844396582 5337543885 6909411303 1509526179 3780029741 2076651479 3942590298 9695946995 5657612186 5619673378 6236256125 2163208628 6922210327 4889218654 3648022967 8070576561 5144632046 9279068212 0738837781 4233562823 6089632080 6822246801 2248261177 1858963814 0918390367 3672220888 3215137556 0037279839 4004152970 0287830766 7094447456 0134556417 2543709069 7939612257 1429894671 5435784687 8861444581 2314593571 9849225284 7160504922 1242470141 2147805734 5510500801 9086996033 0276347870 8108175450 1193071412 2339086639 3833952942 5786905076 4310063835 1983438934 1596131854 3475464955 6978103829 3097164651 4384070070 7360411237 3599843452 2516105070 2705623526 6012764848 3084076118 3013052793 2054274628 6540360367 4532865105 7065874882 2569815793 6789766974 2205750596 8344086973 5020141020 6723585020 0724522563 2651341055 9240190274 2162484391 4035998953 5394590944 0704691209 1409387001 2645600162 3742880210 9276457931 0657922955 2498872758 4610126483 6999892256 9596881592 0560010165 5256375678 <...>
* красным цветом отмечена Точка Фейнмана — последовательность из шести девяток, начинающаяся с 762 цифры числа π. Носит имя американского физика Ричарда Фейнмана (1918—1988), заявившего во время лекции, что он хотел бы запомнить цифры числа π до этой позиции и заканчивать рассказ кому-либо этой последовательности словами «девять, девять, девять, девять, девять, девять и так далее», иронически предполагая, что значение π рационально. Следующая комбинация шести цифр подряд, опять девяток, в числе π встречается на позиции 193034. На позиции 222299 можно найти шесть восьмёрок. Ноль повторяется шесть раз в позиции 1699927. Последовательность же «12345678» встречается уже в позиции 186557266. Последовательность цифр «141592», которая находится сразу после запятой, повторяется в позиции 821582. Последовательность «123456789», можно встретить уже только на позиции 523551502. Кстати, первые шесть цифр числа π, 314159, появляются не менее шести раз среди первых десяти миллионов знаков после запятой числа π.
Числовой ряд, на фоне которого в заставке пролетает корабль Межпланетного экспресса в мультфильме «Футурама: Игра Бендера», является записью числа π, на что указывают шесть идущих подряд девяток.
**Число π считают магическим, так как первые 1440 цифры после запятой заканчиваются цифрами 666, которые упоминаются в Библии как «дьявольское число» или «число зверя».
***Так как 360 градусов в полном круге и число π тесно связаны, некоторые математики пришли в восторг, узнав, что цифры 3, 6 и 0 находится на триста пятьдесят девятом разряде после запятой в числе π.
 |
| картина I века до н.э., нарисованная самим Витрувием |
История числа π шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода:
- древний период, в течение которого π изучалось с позиции геометрии,
- классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке,
- и эра цифровых компьютеров.
  |
| Фрагменты папируса Ринда |
 |
| Двухкартинный комплексный чертёж двухпирамидной системы Хеопса-Голода с их эллипсоидами, крестовыми сводами, габаритной пирамидой и развертками боковых поверхностей |
 |
| переложите одну спичку так, чтобы равенство стало верным |
- Они равны.
- Почему?
- Каждое из них равно π.
А.А.Власов. Из Экзаменационного билета.
По-видимому, в Танахе, в третьей книге Царств (Библия), предполагается, что π=3, что является гораздо более худшей оценкой, чем имевшиеся на момент написания (600 год до н. э.). Ведический же текст «Шатапатха-брахмана» даёт π как 339/108 ≈ 3,139. В эллинистическую эпоху считалось, что π=22/7 и этим значением пользовались и Леонардо да Винчи, и Галилео Галилей. Однако оба приближения очень грубы. Геометрический рисунок, изображающий окружность, описанную около правильного шестиугольника и вписанную в квадрат, сразу дает простейшие оценки для π: 3 < π < 4.
Первый шаг в изучении свойств числа π сделал Архимед (Άρχιμήδης, Archimedes, 287–212 до н. э.). В сочинении «Измерение круга» Архимед, рассматривая правильный 96-угольник, вывел знаменитое неравенство 3 + 10/17 < π < 3 + 1/7 и предположил, что π примерно равняется 22/7 ≈ 3,142857142857143, т.е π лежит в интервале длиной 1/497. В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14… Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней. В том же сочинении, последовательно удваивая число сторон квадрата, Архимед нашел формулу площади круга S = π R2. Позднее он дополнил ее также формулами площади сферы S = 4 π R2 и объема шара V = 4/3 π R3. Именно поэтому число π часто называют «круговой постоянной» и «архимедовой константой».
 |
| Картина Thomas Degeorge (1815) |
 |
| Чжан Хэн |
Чжан Хэн во II веке уточнил значение числа π, предложив два его эквивалента: 1) 92/29 ≈ 3,1724…; 2) √10 ≈ 3,1622.
Около 265 года н.э. математик Лю Хуей из царства Вэй предоставил простой и точный итеративный алгоритм для вычисления π с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для π по следующему принципу:
Позднее Лю Хуей придумал быстрый метод вычисления π и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.
В 480-х годах китайский математик и астроном Цзу Чунь Чжи продемонстрировал, что π ≈ 355/113 (мнемоника, кстати, очень простая: дважды написать нечетные числа: 11 33 55, а потом, разделив их пополам, поместить первое в знаменатель дроби, а второе – в числитель), и показал, что 3,1415926 < π < 3,1415927, используя алгоритм Лю Хуея применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа π в течение последующих 900 лет.
В Индии Ариабхата и Бхаскара использовали приближение 3,1416. Варахамихира в VI веке пользуется в «Панча-сиддхантике» приближением √10.
 |
| слева первая страница книги "Китаб аль-джебр" |
 |
| слева: Самарканд. 1929 г. Внешний вид остатков обсерватории Улугбека; справа - ал-Каши |
Затем, в начале XVII в., голландский математик из Кёльна Лудольф ван Цейлен (1540-1610) вычислил π с точностью до 20-ти десятичных цифр. Удваивая по методу Архимеда число сторон вписанных и описанных многоугольников, он дошел до 60⋅229-угольника. На вычисление ему понадобилось 10 лет. После смерти в его рукописях были обнаружены ещё 15 точных цифр числа π. С тех пор (год публикации 1615) значение π с 32 десятичными знаками получило название «лудольфово число» или «константа Лудольфа». Согласно легенде, эти цифры были выгравированы согласно завещания на его надгробной плите после смерти. И, наконец, в 1706 году англичанин Джон Мечин (John Machin, 1680–1751) впервые смог найти 100 знаков π. Сегодня находят миллионы знаков π с помощью суперкомпьютеров. Чуть ли не каждый год устанавливаются новые рекорды знаков π, но, в отличие от 100 знаков Мечина (см. далее), вопрос о достоверности таких вычислений всегда остается открытым.
Формула длины окружности и 3 формулы Архимеда (для площади круга, площади сферы и объема шара) не являются конструктивными — они не содержат способа вычисления входящего в эти формулы числа π. Если применить известные в интегральном исчислении методы нахождения длины кривой, площади поверхности и объема тела к формулам для окружности, круга, сферы и шара, то можно доказать, что в каждой из этих формул π задается интегралом
Существующие методы вычисления интегралов позволяют таким образом находить π. (Кстати, полученная для π интегральная формула служит исходным пунктом для вывода так называемого распределения вероятностей Коши–Лоренца, хорошо известного в теории вероятностей и имеющего важные приложения в теоретической физике.)
Преобразуя то же самое интегральное выражение, несложно получить представление π в виде либо бесконечной суммы (ряда)
либо бесконечного произведения:
Первую формулу нашли независимо шотландец Джеймс Грегори (James Gregory, 1638–1675) и немец Готфрид Вильгельм Лейбниц (Gottfried Wilhelm Leibniz, 1646–1716). Вторую формулу получил знаменитый криптограф Кромвеля (Oliver Cromwell, 1599–1658) англичанин Джон Валлис (John Wallis, 1616–1703).
Одним из первых, кто представил метод, отличный от метода Архимеда, был Франсуа Виет (1540-1603 гг.). Он пришел к результату, что круг, диаметр которого равен единице, имеет площадь:
С другой стороны, площадь равна π/4. Подставив и упростив выражение, можно получить следующую формулу бесконечного произведения для вычисления приближенного значения π/2:
Полученная формула представляет собой первое точное аналитическое выражение для числа π. Кроме этой формулы, Виет, используя метод Архимеда, дал с помощью вписанных и описанных многоугольников, начиная с 6-угольника и заканчивая многоугольником с 6⋅216 сторонами приближение числа π с 9 правильными знаками.
Английский математик Уильям Броункер (1620-1684 гг.), используя цепную дробь, получил следующие результаты вычисления π/4:
К сожалению, пользы от подобных формул было немного: чтобы вычислить 10 знаков π, необходимо сложить или умножить миллиарды слагаемых или перемножить миллиарды сомножителей, в чем легко убедиться, попытавшись вычислить π таким образом. Такая работа трудна даже для современного мощного компьютера.
Однако процесс вычисления можно ускорить, и тогда использование этих формул приобретает совсем другой смысл. Например, английский математик Джон Мечин (1686-1751 гг.) в 1706 году существенно ускорил вычисления по формуле Грегори–Лейбница, приведя формулу
к виду
и разложив арктангенс по формуле:
В этом случае десять знаков π находятся быстро. Именно эта формула помогла Мечину найти 100 знаков π. Сегодня открыто много аналогов формулы Мечина, по которым π вычисляется еще быстрее. Приведу только 1 из примеров:
Чем меньше аргументы арктангенсов, тем быстрее вычисляется π. Чем меньше максимальный аргумент арктангенсов в аналоге формулы Мечина, тем выше скорость сходимости этого аналога.
Современник сэра Исаака Ньютона (Sir Isaac Newton, 1643-1727) японский математик Секи Такакадзу (Takakazu Shinsuke Seki, 1642–1708) придумал метод ускорения медленно сходящихся последовательностей. Например, известные последовательности правильных многоугольников сходятся к окружности медленно, из-за этого медленно сходятся к числу π последовательности его приближений, рассчитанные с помощью этих многоугольников. Такакадзу ускорил сходимость последовательностей приближений и нашел десять знаков числа π. Прошло более двух столетий, когда английский математик Александр Крэг Эйткен (Alexander Craig Aitken, 1895–1967) переоткрыл метод ускорения сходимости последовательностей, известный сегодня как метод Эйткена. Метод Такакадзу-Эйткена творит чудеса. Если в формуле Грегори–Лейбница сложить 7 слагаемых, то мы найдем только один правильный знак: π = 3,…. Если же к этим семи слагаемым применить метод ускорения, то получим 6 правильных знаков: π = 3,14159… Попутно Такакадзу независимо от Ньютона открыл метод касательных для решения уравнений, первым в мире изучал определители второго и третьего порядка, а также открыл числа Бернулли раньше самого Якоба Бернулли (Jacob Bernoulli, 1654–1705), именем которого они названы.
 |  |
| Виллеброрд Снеллиус | Христиан Гюйгенс |
Важным достижением в изучении числа π было выяснение его теоретико-числовой природы. В 1761 году немецкий математик, физик и астроном Иоганн Генрих Ламберт (Johann Heinrich Lambert, 1728–1777) путём разложения тангенса в непрерывную дробь доказал иррациональность числа π. Это означает, что π нельзя представить в виде дроби. Но можно найти бесконечную последовательность дробей приближающих π, в определенном смысле, наилучшим образом. Такие дроби называются подходящими и строятся в рамках теории цепных или, что то же самое, непрерывных дробей. Ламберт нашел для π первые 27 подходящих дробей. Выпишем здесь только первые 7 из них:
Первая, вторая и четвертая дроби уже рассматривались выше (и это не случайно).
В год доказательства иррациональности π немецкий астроном Иоганн Даниель Тициус (Johann Daniel Titius, 1729–1796) опубликовал закон планетных расстояний, в котором неожиданно появляется последовательность Архимеда, сыгравшая важную роль в доказательстве знаменитого неравенства для π. Приняв расстояние Сатурна от Солнца за 100 единиц, Тициус представил расстояния планет от Солнца согласно таблице. Знаком вопроса отмечено место, где, как предполагал Тициус, предстоит что-то открыть. Интересно, что Ламберт в 1761 году поставил следующий вопрос: «Кто знает, нет ли недостающих планет в обширном пространстве между Марсом и Юпитером, которые будут когда-нибудь обнаружены?». В XIX веке в этом месте открыли кольцо астероидов. Мы видим, что последовательность Тициуса для планетных расстояний получается в результате суммирования последовательности Архимеда с постоянной последовательностью четверок. Позднее этот закон стали называть законом Тициуса–Боде, несмотря на то, что открыл его только один человек — Тициус.
| Планета | Расстояние |
|---|---|
| Меркурий | 4 |
| Венера | 4+3=7 |
| Земля | 4+6=10 |
| Марс | 4+12=16 |
| ? | 4+24=28 |
| Юритер | 4+48=52 |
| Сатурн | 4+96=100 |
В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π².
В последующие годы уточнения значения числа π происходили все быстрее и быстрее. Так, например, в 1794 году Георг Вега (1754-1802) определил уже 140 знаков, из который только 136 оказались верными. Британский математик Уильям Шэнкс прославился тем, что, потратив 15 лет своей жизни, вручную подсчитал число π до 707 знака в 1873 году. Однако позже выяснилось, что 527-е число ошибочно, и, следовательно, все цифры за ним также. (В 1958 году компьютер IBM правильно посчитал все 707 знаков за 40 секунд.)
Наконец, 12 апреля 1882 г., в день своего тридцатилетия, немецкий математик член Баварской академии наук Карл Луис Фердинанд Линдеман (Ferdinand von Lindemann, 1852–1939), используя результаты, полученные признанным лидером математиков Франции во второй половине XIX века Шарлем Эрмитом, доказал, что π – трансцендентное число. Это означает, что π не может быть корнем какого-либо полиномиального уравнения (многочлена) с рациональными коэффициентами — то есть не является алгебраическим числом.
"Природные свойства быстрее всего утрачиваются в большом городе. Причину этого надо искать не в этике, а в геометрии. Прямые линии улиц и зданий, прямолинейность законов и обычаев, тротуары, никогда не отклоняющиеся от прямой линии, строгие, жесткие правила, не допускающие компромисса ни в чем, даже в отдыхе и развлечениях, — все это бросает холодный вызов кривой линии Природы. Поэтому можно сказать, что большой город разрешил задачу о квадратуре круга" (О'Генри, "Квадратура круга").
После того как Линдеман доказал трансцендентность числа π, насущность решения проблемы «квадратуры круга», т.е. классической задачи о построении с помощью циркуля и непроградуированной линейки квадрата с площадью равной площади данного круга, мучившей поколения математиков в течение 24-х веков, начиная с Египета и Вавилона (математики которого, кстати, обнаружив в процессе вычислений числа π, что радиус окружности в качестве хорды входит в нее 6 раз, поделили круг, а заодно и орбиту Солнца, на 360 градусов, решив, таким образом, считать, что в году 360 дней), отпала сама собой как нерешаемого.
 |
| Квадратриса |
 |
| Уравнение кривой в прямоугольных координатах |
- Невозможно точно согласовать движение отрезков ВС и АВ, если не знать заранее отношение длины дуги четверти окружности к радиусу, поэтому получается порочный круг.
- Точку К построить нельзя, потому что в соответствующий момент времени отрезок и радиус совпадают. В современной терминологии, точка К есть предел точек квадратрисы — понятие, чуждое античной математике.
 |
| Схема квадратуры круга с помощью квадратрисы |
Стоит также указать на связь числа π с многомерными сферами и шарами. Сферой в n-мерном евклидовом пространстве называется множество точек этого пространства, удаленных от данной точки на расстояние R. Шаром в n-мерном евклидовом пространстве называется множество точек этого пространства, удаленных от данной точки на расстояние, не превышающее R. Объем n-мерной сферы и объем n-мерного шара пропорциональны Rn. Объем одномерной сферы – это длина окружности, а объем двумерной сферы – это площадь обычной сферы. Объем одномерного шара – это длина отрезка, объем двумерного шара – это площадь круга, а объем трехмерного шара – это объем обычного шара. Объёмы многомерных шаров удовлетворяют рекуррентному соотношению
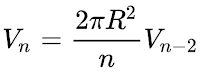 , а площади их поверхностей соотносятся как
, а площади их поверхностей соотносятся как  . Известные формулы для окружности, круга, сферы и шара не содержат способа вычисления входящего в эти формулы числа π. Поэтому при работе с этими формулами необходимо каким-то образом дополнительно задать π. Но вот что интересно. Если мы рассмотрим все множество формул для многомерных сфер и шаров, позволяющих находить их объемы, то при работе с этими формулами нет необходимости задавать π дополнительно. Дело в том, что, при естественном условии монотонности последовательности отношений объемов n–мерных шаров и n–мерных сфер для всех натуральных значений n, сами формулы однозначно определяют числовое значение π.
. Известные формулы для окружности, круга, сферы и шара не содержат способа вычисления входящего в эти формулы числа π. Поэтому при работе с этими формулами необходимо каким-то образом дополнительно задать π. Но вот что интересно. Если мы рассмотрим все множество формул для многомерных сфер и шаров, позволяющих находить их объемы, то при работе с этими формулами нет необходимости задавать π дополнительно. Дело в том, что, при естественном условии монотонности последовательности отношений объемов n–мерных шаров и n–мерных сфер для всех натуральных значений n, сами формулы однозначно определяют числовое значение π.Эра компьютерных вычислений
В начале XX века индийский математик Сриниваса Айенгор Рамануджан* (ஸ்ரீனிவாஸ ராமானுஜன் ஐயங்கார், 1887-1920) обнаружил множество новых формул для числа π, о которых говорили, что ни у кого другого не «хватило бы воображения, чтобы их изобрести»*, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. В 1910 году он получил формулу для вычисления π через разложение арктангенса в ряд Тейлора. При k=100 достигается точность в 600 верных цифр числа π.
* Результаты Сринивасы были неожиданными и красивыми, но по характеру творчества он радикально отличался от других математиков. Он не знал, что такое доказательство. Его результаты были итогом чисто интуитивного прозрения и часто приходили во сне: ему диктовала их богиня Наматжири, прародительница богов, участвовавшая в создании из глины первых людей. Поразительно было как то, что большинство его формул оказывались верными, так и то, что иногда богиня ошибалась. При этом формулы были воистину красивыми и загадочными. В этом отношении существуют восхитительные спекуляции по поводу «феномена» Рамануджана. В одной из популярных книжек было высказано предположение, что математика сейчас есть функция левосторонней части мозга, определяющей аналитические способности человека. Но вполне возможно, что в период, когда доминирующей была правосторонняя часть мозга, ответственная за чувственные восприятия, человек познавал «непосредственно». И тогда можно предположить, что Рамануджан являлся «осколком» той древней цивилизации, которая развивала математику совсем по другому пути. Впрочем, эта романтическая догадка так и остается догадкой.
Эпоха цифровой техники (ЭВМ) в XX веке позволила существенно увеличить точность получаемых значений числа π при увеличении скорости рассчетов. В 1949 году всего за 70 часов с помощью ENIAC (Electronic Numerical Integrator and Computer) группа ученых под руководством Джона фон Неймана (1903-1957) получила 2037 знаков после запятой числа π. В 1954 г. в Южной Каролине С.К.Николсон и Дж.Джинел (Jeenel), используя NORC (IBM Naval Ordnance Research Calculator - единственный в своем роде компьютер первого поколения (на электронных лампах), созданный IBM для Управления артиллерийского вооружения ВМС США) за 13 минут вычислили 3093 знака после запятой, в 1957 г в Лондоне ученый-компьютерщик Джордж Эрик Фелтон на одном из первых британских ламповых компьютеров Ferranti Pegasus вычислил 10021 знак, из которых правильными были 7480, а в 1959 г. в Париже Франсуа Женюи на машине IВМ 704, в которой была впервые применена память на ферритовых сердечниках и аппаратное арифметическое устройство с плавающей точкой, за 4,3 часа счета вычислил 16167 знаков числа π. Но уже в 1961-м американские математики Дэниэл Шенкс и Джон Уильям Ренч-младший за 9 часов работы компьютера IBM 7090 вычислили более 100000 знаков десятичного разложения π. Такой прогресс имел место не только благодаря быстрому развитию аппаратного обеспечения, но и благодаря алгоритмам: одним из самых значительных результатов было открытие в 1960 году быстрого преобразования Фурье, что позволило быстро осуществлять арифметические операции над очень большими числами. В 1973 году французами Жаном Гийу и Мартином Буйе на компьютере CDC-7600 была пройдена отметка в миллион знаков (1 001 250 знаков). Работа заняла меньше одного дня.
 |
| братья Чудновские |
вычисляющая по 14 цифр за ход. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении π в конце 1980-х, включая тот, в результате которого в 1989 году было получено 1011196691 цифр десятичного разложения. В 1991 году Чудновские добились новых 2260000000 десятичных знаков константы, а в 1994 — 4044000000. После этого количество верных знаков числа π нарастало лавинообразно. Позже формула применялась для установления первого рекорда на персональном компьютере Фабрисом Белларом. Эта формула и сегодня используется в программах, вычисляющих π на персональных компьютерах.
Важным событием стало открытие Саймоном Плаффом в 1995 году формулы, позволяющей извлечь любую шестнадцатеричную цифру числа π без вычисления предыдущих. Формула носит название «Формула Бэйли — Боруэйна — Плаффа» в честь авторов статьи, где формула была впервые опубликована.
Используя эту формулу, а также формулы Мэчина и Брента—Саламина, профессор информатики Токийского университета Ясумаса Канада на суперкомпьютере Hitachi SR 8000/MPP (64 процессора, скорость вычислений — 2 триллиона операций в секунду, оперативная память — 1 терабайт) 6 декабря 2002 года за 600 часов счета получил 1 241 100 000 000 знаков (более 1 триллиона) числа π после запятой. Ясумаса занимался вычислением значения числа π и ранее: в 1981 году он получил до двух миллионов знаков после запятой, в 1995 — 6 миллиардов, в 1997 — 51 539 600 000, в 1999 — 206 158 430 000.
В 2006 году Саймон, используя PSLQ, получил несколько красивых формул для вычисления π. Например,
где q=eπ.
В 2009 году учёные из японского университета Цукубы под руководством профессора математики Дайсуке Такахаши, используя T2K Open Tsukuba System Supercomputer (640 узлов (четырех-ядерных процессоров AMD Opteron), скорость одного узла 147,2 гигафлопс, что обеспечило производительность в 95 триллионов операций с плавающей точкой в секунду, память компьютера 13,5 терабайт) и алгоритм Гаусса-Лежандра, за 73 часа 36 минут вычислили число π с рекордной точностью 2576980377524 (2 с половиной триллиона) знака после запятой. Исследователи подали заявку на включение своего достижения в Книгу рекордов Гиннесса.
31 декабря 2009 года французский программист Фабрис Беллард на персональном компьютере (процессор Core i7 с тактовой частотой 2,93 ГГц, 6 ГБ ОЗУ, 7,5 ТБ дискового пространства с использованием пяти жестких дисков по 1,5 ТБ (модель Seagate Barracuda 7200.11)) под управлением 64-битной Red Hat Fedora 10 за 131 день рассчитал последовательность из 2 699 999 990 000 десятичных разрядов. Для проверки двоичных цифр использовалась сеть из 9 настольных ПК в течение 34 часов, алгоритм Чудновского. Достижение Беллара показало, что для таких вычислений не обязательно иметь суперкомпьютер.
17 сентября 2010 года сотрудник компании «Yahoo» математик Николас Чже смог вычислить в числе π 2 квадрильона знаков после запятой (2x1015). Для того, чтобы просто записать все это на бумаге, потребуется бумажная лента больше двух миллиардов километров длиной. Если развернуть такую запись, ее конец выйдет за пределы Солнечной системы. Если бы эта работа велась на единственном компьютере, она потребовала бы более 500, но Чже использовал технологию так называемых облачных (или рассеянных) вычислений Hadoop, на которую завязана тысяча компьютеров Yahoo, с применением созданного фирмой Google метода, известного под названием MapReduce, суть которого состоит в том, что большая - в несколько петабайт - задача разбивается на множество малых, и таким образом решаются математические уравнения, к которым иначе попросту невозможно подступиться - и даже при этом на калькуляцию у него ушло 23 дня. "Интересно, что посредством определенных алгебраических манипуляций наша формула в состоянии вычислять π, пропуская некоторые фрагменты. Другими словами, это позволяет определять отдельные части π, - объяснил Чже в интервью BBC. Как прокомментировал данное событие Фабрис Беллард в том же интервью: "Вычисления всего числа м и определение отдельных цифр из этого числа - задачи совершенно разные. Данный проект - это скорее демонстрация возможностей сети Hadoop... Он способен показать работоспособность новых алгоритмов, которые можно будет использовать в других областях".
 |
| Шигэру Кондо |
 |
| График, показывающий, как точность числовых приближений к числу π, измеренному в десятичных разрядах (в логарифмической шкале), развивалась в истории человечества. Время до 1400 сжато. |
К известным методам уточнения π (подбором деления пар чисел, вписывания в круг многоугольника и вычисления сумм рядов) во второй половине ХХ века добавились еще 3, которые можно назвать экспериментальными.
Первый, так называемый "метод иглы Бюффона", который был предложен Бюффоном (графом Жоржем-Луи Леклерком де Бюффоном, французским натуралистом, биологом, математиком, естествоиспытателем и писателем, создателем первого в истории европейской науки подлинно научного и философского труда по зоологии — «Естественной истории» («Histoire naturelle, générale et particulière», 1749-1788, в 36 томах), в котором были описаны все известные к тому времени виды млекопитающих и птиц) еще в 1777 году. В нем на разлинованную равноудаленными параллельными прямыми плоскость произвольно бросается игла, длина которой L равна половине расстояния r между соседними прямыми. (Так что игла либо не пересекает прямые, либо пересекает ровно одну при каждом бросании). Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросаний стремится к π при увеличении числа бросаний до бесконечности. Нужно сделать очень много испытаний, чтобы получить более-менее приличную точность приближения полученной дроби к π, а кроме того, при эксперименте надо внимательно следить, чтобы бросание иглы было "равновероятным": метод иглы Бюффона существенным образом базируется на методах теории вероятностей. Подробно с экспериментом можно лзнакомиться в журнале «Hard’n’Soft” №8 2001, статья Андрея Теплякова “Моделируя жизнь”, где успешно подтвердили первые знаки с помощью метода Монте-Карло. Здесь же скажу, что вероятность (или, точнее, математическое ожидание количества пересечений за один опыт; вероятностью это становится лишь при условии, что r>L) того, что отрезок пересечет прямую, связана с числом π следующим образом:
A - расстояние от начала иглы до ближайшей к ней прямой;
θ - угол иглы относительно прямых.
Этот интеграл просто взять. При условии, что r>L получается решение: p=2L/rπ. Таким образом, подсчитав долю отрезков, пересекающих прямые, можно приближенно определить число π. Как видно, отношение длины окружности к диаметру находят здесь опытным путем, причем, что всего любопытнее, не чертят ни круга, ни диаметра, т.е. обходятся без циркуля. Человек, не имеющий никакого представления о геометрии и даже о круге, может тем не менее определить по этому способу число π, если терпеливо проделает весьма большое число бросаний иглы. При увеличении количества попыток точность получаемого результата будет увеличиваться. Говорят, что швейцарский астроном Р.Вольф в середине XIX века наблюдал 5000 падений иглы на разграфленную бумагу и получил в качестве π число 3,159... — выражение, впрочем, менее точное, чем архимедово число.
Число π можно вычислить, беспорядочно бросив на стол и кучу скрепок. Все, что нужно для этого опыта: листок бумаги, карандаш и горсть скрепок (или игл, гвоздей, или чего-нибудь подобного).
- Нарисуйте на бумаге две параллельные линии длиной примерно в две скрепки. Теперь бросьте горсть скрепок на пространство между строками. Неважно, сколько скрепок вы бросите, но чем больше, тем лучше, поэтому действуйте смелее.
- Возьмите общее количество скрепок, умножьте его на 2, затем разделите это число на количество скрепок, которые касаются одной из линий. Таким образом, если бы вы бросили 20 скрепок, и 13 из них касались одной из линий, то вы разделили бы 40 на 13. Число, которое вы получите, будет близко к π. И если вы увеличите количество скрепок, оно будет становиться ближе и ближе.
Число π можно получить и не обращаясь к инструменту портного. Нарисуем на земле круг и опишем вокруг него квадрат. Бросив наугад несколько камешков, подсчитаем количество тех, что попали внутрь круга, и тех, которые попали внутрь квадрата. Затем, разделив первое на второе и умножив результат на 4, мы получим число… очень близкое к 3,14… Квадратура круга она такая!
Второй метод, придуманный выдающимся математиком-бильярдистом Григорием Александровичем, и называемый π-бильярдом, основан на оригинальной модели. При столкновении двух шаров, меньший из которых находится между большим и стенкой, и больший движется к стенке, число соударений шаров позволяет вычислить π со сколь угодно большой наперед заданной точностью. Надо только запустить процесс (можно и на компьютере) и посчитать число ударов шаров.
Положим на числовую ось два биллиардных шара с массами M и m (M>m), и будем предполагать, что в начале координат х=0 расположена абсолютно упругая стенка, отражающая налетающий на неё шарик. При отражении от стенки скорость шарика меняется на строго противоположную. Размеры шариков несущественны, и для простоты мы будем считать их точечными частицами. Фиксируем натуральное число N. Следующая процедура позволяет определить любое наперёд заданное количество N последовательных цифр числа π
- Массы m и M подбираем так, чтобы M/m=100N
- Шар m располагаем между стенкой х=0 и шаром М
- Запускаем шар М в сторону шара m с произвольной скоростью
- Подсчитываем общее количество ударов в системе (т. е. число столкновений между шарами и число отражений шара m от стенки)
- Записываем полученное число в десятичной системе и обозначаем его через π(N)
а) число ударов в описанной динамической системе всегда конечно и не зависит от начальных положений шаров и начальной скорости шара М.
б) Число π(N) ударов в системе равно
Для третьего метода можно воспользоваться известным предположением теории чисел: вероятность, что 2 числа взаимно просты равна 6/π2. Взаимно простыми называются числа, не имеющие общих делителей (для строгости обычно добавляют “кроме единицы”). Какой же алгоритм наших действий? Берем 2 случайных числа, находим их делители и сравниваем их. Повторяя процесс в цикле, вычисляем долю шагов цикла (от общего числа шагов), при которых числа не имели общих делителей. Разделив 6 на эту долю и извлекши квадратный корень из частного, получим искомое значение π.
Графическое представление числа π. В круге все шито-крыто. Ничего не понятно о сути константы. Во втором случае видно, как образовано это число. Площадь трапеции, выделенная при помощи красной наклонной прямой, равна ровно трем. Иррациональность и транцендентность числу π придает маленькая верхняя шапочка. Весь сыр-бор на протяжении тысячелетий как раз и шел вокруг точности определения площади шапочки.
Есть еще один забавный способ вычисления (точнее, измерения) числа π - взвешивание. Да-да, вы не ослышались. Число π можно взвесить. Для этого вырезать из любого доступного вам материала (бумага, картон, пластик, стекло, жесть, алюминий, сталь, дерево, ДСП, ДВП, фанера, прескартон, ткань и т.д.) квадрат со стороной, длина которой равна R. Взвесить полученный квадрат. После этого обрезать его углы, чтобы получился круг, и взвесить полученную фигуру. После этого приступаем к рассчетам. Из курса физики нам известно, что масса (m) равна произведению объма (V) на плотность (ρ): m = ρ × V. В свою очередь, из курса стереометрии, известно, что объем цилиндра (а так же призмы, которая, как известно, является частным случаем цилиндра) равен площади (S) основания фигуры, умноженой на ее высоту (h): V = S × h. Таким образом, m = ρ × S × h. Из курса геометрии известно, что площадь квадрата равна: Sкв = R2, а площадь круга - Sкр = π(R/2)2=πR2/4. Подставим данные формулы в формулы масс соответствующих фигур: mкв = ρ × R2 × h и mкр = ρ × πR2/4 × h. Теперь разделим обе части друг на друга. После упрощения получим формулу: mкр/mкв=π/4, или π = 4mкр/mкв.
 |
| панциферная формула (т.е. использующая каждую цифру только по одному разу) числа π |
Однако вычисление значения π является лишь малой частью его истории. Это число обладает свойствами, благодаря которым эта константа столь любопытна! В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
В настоящее время с π связано ряд до сих пор не решенных задач. Например, не решен вопрос о нормальности этого числа. Нормальным (n-нормальным) называются трансцендентные числа, в записи которых по основанию n любая фиксированная группа цифр встречается с одной и той же вероятностью. Более того, до сих пор не известно, все ли цифры от 0 до 9 встречаются в десятичной записи числа π бесконечное число раз. Так же до сих пор неизвестно, являются ли числа π+e, π/e или lnπ (e — это еще одно иррациональное трансцендентное число) иррациональными. Появляется много соотношений, не связаных с окружностями. Эта часть коэффициента нормализации нормальной функции, видимо, наиболее широко используемой в статистике. Число π появляется как сумма многих рядов и равно бесконечным произведениям, оно важно и при изучении комплексных чисел.
В физике его можно найти (в зависимости от применяемой системы единиц) в космологической постоянной (самая большая ошибка Альберта Эйнштейна) или константе постоянного магнитного поля. В системе счисления с любым основанием (в десятичной, двоичной…), цифры π проходят все тесты на случайность, не наблюдается никакого порядка или последовательности. Дзета-функция Римана тесно связывает число π с простыми числами. Это число с долгой историкй наверняка до сих пор хранит множество сюрпризов.
 |
| Круги на полях 2008 года |
А это уже земляне постарались:
 |
| в Кругу закодировано изображение первых десяти знаков числа π |
Стоунхендж же отражает путь Сириуса-Ориона на небе. Так вот путь числа π в небе называют щитом Осириса-Ориона. То есть связь с драконидами.
  |
| хотя у греков они зовутся Ἡράκλειοι Στῆλαι |
В ноябре 2006 года (открытие 1 декабря 2006 года) на зеркальных стенах пешеходного тоннеля Opernpassage западной ветви метро, что в Старом Городе в Вене, была установлена работа Pi художника Кена Лума (Ken Lum) из Ванкувера (Канада), посвященная кроме прочего числу π, изображенному с точностью 478 знаков после запятой. В дополнение к числу π, дисплей общей длинной 130 метров отображает в 16 фактоидов (различных статистических данных), передаваемых в реальном времени, таких как количество населения мира, число голодающих детей во всем мире и рост Сахары с начала года, а также менее серьезных, такие как количество съеденных венцами рыбных шницелей в текущем году и текущее число влюбленных в Вене. Научные данные, собранные Лумом совместно с Институтом SORA (Southern Rails (Южная Железная Дорога) Cooperative Ltd. ), ответственным за проект в концепции исследования и расчета алгоритмов. С тех пор SORA обновляет данные ежегодно раз в год. Целью данного проекта было показать, что современное искусство в состоянии соединить искусство с наукой, архитектурой и социологией, а так же превратить Карлсплатц в "живое место для встреч с коммуникативной художественной харизмой".
 |
| Если диаметр окружности равен 1, её длина равна π |
 |
| Если радиус окружности равен 1, её длина равна 2π |
Кстати, если вы тоже не знаете, почему стучат колёса, то анекдот вам в помощь:
Двое едут в поезде. Один говорит:
– Странно, колёса круглые, рельсы прямые, откуда стук?
– Как откуда? Колёса-то круглые, а площадь круга - пи эр квадрат. Вот квадрат-то и стучит!
 |
| пародист А.А.Иванов |
Площадь круга... Площадь круга... Два пи эр.
— Где вы служите, подруга?
— В АПН. [АПН – Агентство печати Новости в СССР]
К чести представителей поэтического корпуса, на эту математическую ошибку очень едко указал известный советский поэт и пародист Александр Иванов [Иванов А.А. Плоды вдохновения. – М., «Советский писатель», 1983, 224 с.] (кстати, юмористическая передача, которую он вёл, также была связа с кругом, она называлась "Вокруг смеха"):
Заколдованный круг
Говорит моя подруга, чуть дыша:
— Где учился ты, голуба, в ЦПШ1?
Чашу знаний осушил ты не до дна,
Два пи эр — не площадь круга, а длина,
И не круга, а окружности притом;
Учат в классе это, кажется, в шестом.
Ну поэты! Удивительный народ!
И наука их, как видно, не берет.
Их в банальности никак не упрекнешь,
Никаким ключом их тайн не отомкнешь.
Все б резвиться им, голубчикам, дерзать.
Образованность все хочут показать...
1Церковноприходская школа
* Праздник, танцы на площади
Как мы кружимся — и я, и он, и все!
Вместо солнца — просто белка в колесе.
Над толпою — как мембрана — медный бас,
он проигрывает, проигрывает нас,
как пластинку, как пластинку, как тогда —
в патефонные далекие года.
Площадь круга... Площадь круга... Два пи эр...
— Где вы служите, подруга?
— В АПН.
— Вам не кажется, что мы сейчас в Гель-Гью?
— Вы банальны, друг мой, Грина не терплю...
Грины, Грэмы и Эльмары — все потом!
Солнце машет нам оранжевым хвостом.
Где часы и где минуты, где века?
Лишь полоска на руке от ремешка...
— Вам не кажется, что все идет кругом?
— Мы сейчас столкнемся...
— С другом иль с врагом? —
Все мы кружимся — Господь нас пронеси, —
все немножечко вокруг своей оси.
На большом на барабане целый час,
как на лобном месте, распинают вальс.
— Загорел на вашей ручке ремешок...
Что со мной? Во мне проснулся пастушок,
и гусар, который спит во мне давно,
и кому еще проснуться суждено.
— Вам не кажется, что мне пора домой?
— О, конечно! Но нельзя же по прямой,
а вращенье в этой солнечной гульбе —
лучший способ возвращения к себе.
Числа π и е входят во множество формул в математике, физике, химии, биологии, также в экономике. Впервые число π вышло за пределы круга и стало применяться в математических кривых, таких как гипоциклоида, и в архитектуре, например, при строительстве арок, в XVII веке. Произошло это после того, как обнаружили, что в данных областях некоторые величины могут быть выражены через само число π. В ХХ веке число π уже использовалось во многих математических областях, таких как теория чисел, вероятности и хаоса. Значит, они отражают какие-то общие законы природы. Какие именно? Определения этих чисел через ряды, несмотря на их правильность и строгость, все же оставляют чувство неудовлетворенности. Они абстрактны и не передают связи рассматриваемых чисел с окружающим миром посредством повседневного опыта. Между тем можно утверждать, что константа е непосредственно связана с однородностью пространства и времени, а π - с изотропностью пространства. Тем самым они отражают законы сохранения: число е - энергии и импульса (количества движения), а число π - вращательного момента (момента импульса). Обычно столь неожиданные утверждения вызывают удивление, хотя по существу, с точки зрения теоретической физики, в них нет ничего нового. Глубинный смысл этих мировых констант остается terra incognita для школьников, студентов и, по-видимому, даже для большинства преподавателей математики и общей физики, не говоря уже о других областях естествознания и экономики.
Сформулируем первый основной тезис, и поясним его смысл и следствия.
1. Число π отражает изотропность свойств пустого пространства нашей Вселенной, их одинаковость по любому направлению. С изотропностью пространства связан закон сохранения вращательного момента.
Отсюда вытекают общеизвестные следствия, которые изучают в средней школе.
Следствие 1. Длина дуги окружности, вдоль которой умещается ее радиус, составляет естественную дуговую и угловую единицу радиан.
Эта единица безразмерная. Чтобы найти число радианов в дуге окружности, надо измерить ее длину и разделить на длину радиуса этой окружности. Как мы знаем, вдоль любой полной окружности ее радиус укладывается приблизительно 6,28 раза. Точнее, длина полной дуги окружности составляет 2π радиан, причем в любых системах счисления и единицах длины. Когда изобретали колесо, оно получалось одинаковым и у индейцев Америки, и у кочевников Азии, и у негров Африки (ой, пардон, у афроафриканцев). Только единицы измерения дуги были разными, условными. Так, наш угловой и дуговой градус был введен вавилонскими жрецами, посчитавшими, что диск Солнца, находящегося почти в зените, укладывается 180 раз на небосводе от рассвета до заката. 1 градус ≈ 0,0175 рад или 1 рад ≈ 57,3°. Можно утверждать, что и гипотетические инопланетные цивилизации без труда поняли бы одна другую, обменявшись посланием, в котором окружность разделена на 6 частей "с хвостиком"; это означало бы, что "партнер по переговорам" уже как минимум прошел стадию изобретения колеса и знает, что такое число π.
Предположим, не только мы хотим установить контакт с разумными существами других звёздных систем, но и они с нами. На какую частоту следует настроить наши приёмники, чтобы шансы на контакт были максимальными? Пётр Васильевич Маковецкий в остроумной и увлекательной книге “Смотри в корень!” утверждает, что искомая частота должна равняться произведению частоты нейтрального водорода на число π. Выбор продиктован тем, что водород должен быть знаком каждому инопланетянину, поскольку заполняет всю нашу Галактику. Что касается π, то П.В.Маковецкий выдвигает основополагающий тезис: “Природа не умеет умножать частоту на иррациональное число!” То есть ясно: такая частота может исходить только от разумных существ. Но этого мало: “Число – один из главных признаков нашей цивилизации и нам подобных. Это пароль разума, подобного нашему. Цивилизация, не знающая π, не имеет математики и радиотехники. Она не может сегодня вступить с нами в контакт, да с нею пока что нам, видимо, и не о чём говорить”.
Кстати, учёные в романе знаменитого американского астрофизика и писателя, одного из ведущих специалистов по проблеме общения цивилизаций во Вселенной Карла Сагана «Связь» пытались разгадать довольно точное значение числа π, чтобы найти скрытые сообщения от создателей человеческой расы и открыть людям доступ к "более глубоким уровням вселенских знаний". Карл Саган писал, что такие числа, как π, это, по-видимому, послание, которое нам хотели передать, и которое заложено еще при основании Вселенной.
Следствие 2. Предназначение тригонометрических функций - выражать соотношения между дуговыми и линейными размерами объектов, а также между пространственными параметрами процессов, происходящих в сферически симметричном пространстве.
Из сказанного ясно, что аргументы тригонометрических функций в принципе безразмерны, как и у других типов функций, т.е. это действительные числа - точки числовой оси, которые не нуждаются в градусном обозначении.
Опыт показывает, что школьники, студенты колледжей и вузов не без труда привыкают к безразмерным аргументам у синуса, тангенса и т.д. Далеко не каждый абитуриент сможет без калькулятора ответить на вопрос, чему приблизительно равен cos1 (примерно 0,5) или arctg π/3. Последний пример особенно сбивает с толку. Часто говорят, что это бессмыслица: "дуга, арктангенс которой равен 60°". Если сказать именно так, то ошибка будет в неправомочном применении градусной меры к аргументу функции. А правильный ответ: arctg(3,14/3) ≈ arctg1 ≈ π/4 ≈ 3/4. К сожалению, сплошь и рядом абитуриенты и студенты говорят, что π = 180°, после чего приходится их поправлять: в десятичной системе счисления π = 3,14…. Но, конечно, можно сказать что π радиан равно 180°.
Разберем еще одну нетривиальную ситуацию, встречающуюся в теории вероятностей. Она касается важной формулы вероятности появления случайной ошибки (или нормального закона распределения вероятностей), в которую входит число π. По этой формуле можно, например, вычислить вероятность падения монеты на герб 50 раз при 100 подбрасываниях. Итак, откуда взялось в ней число π? Ведь никакие круги или окружности там вроде бы не просматриваются. А суть в том, что монета падает случайным образом в сферически симметричном пространстве, по всем направлениям которого и должны равноправно учитываться случайные колебания. Математики так и делают, интегрируя по кругу и вычисляя так называемый интеграл Пуассона, который равен
 и входит в указанную формулу вероятности. Наглядной иллюстрацией таких колебаний служит пример со стрельбой по мишени в неизменных условиях. Дырочки на мишени рассеяны по кругу (!) с наибольшей плотностью около центра мишени, а вероятность попадания можно вычислить по той же формуле, содержащей число π.
и входит в указанную формулу вероятности. Наглядной иллюстрацией таких колебаний служит пример со стрельбой по мишени в неизменных условиях. Дырочки на мишени рассеяны по кругу (!) с наибольшей плотностью около центра мишени, а вероятность попадания можно вычислить по той же формуле, содержащей число π.Кстати, связь между π и другой удивительной величиной — золотым сечением — на самом деле так и не доказана. Люди давно заметили, что «золотая» пропорция — она же число Φ (Фи, названное в честь древнегреческого скульптора и архитектора Фидия, поскольку в пропорциях частей знаменитого храма Афины Парфенона, созданного Фидием, исследователи находят “золотую пропорцию”), в котором Лука Пачоли, современник и друг Леонардо да Винчи, усматривал «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа — и число π, делённое на 2, различаются между собой меньше, чем на 3% (1,61803398... и 1,57079632...). Однако для математики эти 3% — разница слишком существенная, чтобы считать эти значения тождественными. Точно так же можно сказать, что число π и число Фи являются родственниками ещё одной известной постоянной — числа Эйлера, так как корень из него близок к половине числа π. Половина Пи — 1,5708, Фи — 1,6180, корень из Е — 1,6487.
 |
| вот оно, серебряное сечение |
Погода пуще свирепела,
Нева вздувалась и ревела,
Котлом клокоча и клубясь,
И вдруг, как зверь остервенясь,
На город кинулась. Пред нею
Всё побежало, всё вокруг
Вдруг опустело – воды вдруг…
Где рифма к "перед нею"? Может, её тоже смыло наводнением, как домик Параши?
Проверяю по черновому и беловому автографам. Есть строка! Её нет только в писарской копии, которую, впрочем, Пушкин усердно правил. Бегу в Пушкинский дом сверяться с оригиналом.
…Со всею силою своею
Пошла на приступ. Перед нею…
Потерянную писарем строку Пушкин, конечно, заметил. Но восстанавливать не стал. Без неё лучше”.
"ОБ ОДНОЙ СТАРИННОЙ ОШИБКЕ КЛАССИЧЕСКОГО МУЗЫКОВЕДЕНИЯ
Если одну октаву (от ноты до и до следующего до) принять за виток спирали, то малая терция будет соответствовать по частоте ноте ля. Но в темперированном (классическом) строе отношение 5/6 уже не работает: камертонное ля равно 440 герцам, а мы по эталонному до II октавы (523,25 герц) получаем ля I октавы в 436,04 герц.
В XVII столетии создатели темперированного строя разделили октаву на 12 равных интервалов. Они рассуждали так: если от до до до частота ноты удваивается, то темперированный интервал должен быть 12√2. (Умножив 12 раз число 1,0595..., получаем искомую двойку.)
Симфоническая музыка выросла из темперации октавы.
Но, понимая, что темперированная гамма – виток спирали, музыковеды вот уже 3 века не могут уйти от линейных представлений времен позднего Средневековья, хотя все музыканты слышат, что клавишные инструменты почему-то очень плохо звучат рядом со смычковыми.
Можно допустить, что на самом деле темперированный полутон не равен 12√2, но только близок к этому числу. И скрипач, и певец, и человек за роялем – все они настроены природой по числу π, а не по квадратным корням. Потому-то, надо полагать, опытные настройщики всегда перестраивают фортепьяно для игры со смычковыми, чуть повышая (по сравнению с эталонной) частоту каждого следующего до (а на самом деле – каждой ноты).
Отказавшись от сведения трансцендентной пространственно-временной гармонии к иррациональной гармонии диагоналей квадратов, мы откажемся от попытки выразить π через √2. И получим другое решение проблемы темперации и другое определение минорной терции: малая (минорная) терция – это диаметр частотного интервала от данной ноты до аналогичной ноты более низкой октавы, то есть серебряное сечение октавы. В этом случае, взяв эталонные значения до I и II октав, мы получим отклонение от камертонного ля только в 0,02 герца.
Это значит, что интервал каждой октавы надо расширить на несколько центов.
Ньютон разделил цветовую гамму по соотношениям простейшей фригийской гаммы. С тех пор мы и пользуемся архаичным по сути цветовым строем, очень мало соответствующим реальной «музыке сфер» и просто музыке, а значит, и гармонии вообще". (Андрей Чернов. Заметки о вечном)
Запоминание числа π
В общем, Вы, наверняка, уже поняли, что без числа π не обойтись. Но как же его запомнить спросите Вы? Очень даже просто. Не одно поколение постаралось приложить к этому
Например, советский математик и популяризатор науки Яков Перельман создал целый мнемонический диалог:
- Что я знаю о кругах (количество букв в каждом слове соответствует значению числа π - 3,1416 - с учетом округления).
- Вот и знаю я число, именуемое пи — молодец! (3,1415927 - с учетом округления)
- Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3,14159265359 - с учетом округления)
Е.Я.Терсков, учитель средней школы г.Москва, придумал строку: «Это я знаю и помню прекрасно», на что его ученица Эся Чериковер сочинила забавное продолжение: «Пи многие знаки мне лишни, напрасны». Это двустишие позволяет определить 12 цифр (соответственно 3.14159265358).
Или более современная версия: "Она и была, и будет уважаемая на работе" (3,1415926).
* Еще вариант:
Нужно только постараться
И запомнить все, как есть:
Три, черырнадцать, пятнадцать,
Девяносто два и шесть.
* И еще один:
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим -
Это будет пять, три, пять,
Восемь, девять, восемь.
(С. Бобров "Волшебный двурог")
* А вот дореволюционная фраза: "Кто и шутя и скоро пожелаетЪ Пи узнать число, уже знаетЪ" (3,1415926536).
* Это я знаю и помню прекрасно,
Но многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.
* А это, английский стишок для запоминания числа π до двадцатого знака после запятой (3,14159265358979323846):
PIE
I wish I could determine pi
Eureka cried the great inventor
Christmas pudding
Christmas pie
Is the problem's very center.
* Аналогичный английский стишок (двенадцать знаков после запятой - 3.141592653589):
See I have a rhyme assisting
My feeble brain, its tasks offtimes resisting.
* "May I have a large container of coffee?" ("Можно ли мне более емкую посуду для кофе?") (3,1415926)
или как вариант: "May I have a large container of coffee beans?" ("Можно мне большую упаковку кофейных зерен?"), помогающая запомнить восемь знаков после запятой (3,14159265)
* "How I want a drink, alcoholic of course, after the heavy chapters involving quantum mechanics" ("Как же мне хочется выпить, конечно же, алкоголя, после тяжелой работы над главой о квантовой механике")
* И еще один стишок:
Now
I even
I Would celebrate
In rhymes unapt
The great immortal Syracusan
Rivaled nevermore
Who in his wondrous lore
Passed on before
Gave men his guidance
How to circles mensurate
Лимерик Харви Л. Картера (правда не для запоминания цифр числа пи)
Tis a favourite project of mine
A new value of pi to assign.
I would fix it at 3
For it's simpler, you see
Than 3 point 14159.
* Французский вариант (3.141592653589793238462643383279):
Que j'aime faire apprendre un nombre utile aux sages!
Immortel Archim'ede, sublime ing`enieur,
Qui de ton jugement peut sonder la valeur?
Pour moi ton probl'eme eut de pareils avantages.
("Люблю учить я мудрецов полезному числу!
Бессмертный Архимед, великий инженер,
По-твоему, кто сможет значение узнать?
Твоя задача для меня наградою была...").
А швейцарский певец и автор песен, поэт и прозаик на голландском языке Drs. P. (Доктор Пи, Хайнц Херманн Польцер) посвятил запоминанию числа танго "Griekse tango" - драматическую песню, которую можно найти, в частности, в "Drs. P. Compilé sur CD.". В этой песне он поет про первые 8 знаков после запятой: "Таким образом, я нахожу 3,14159265".
* поэма Христиана Ривьеры (Christian Rivière) на эсперанто:
Kun π, ĉiam l'afero konverĝas,
3, 1 4 1 5 9
al nombro utila kaj magia.
2 6 5 3 5
Infinite decimaloj anseras,
8 9 7
ĝiseterne tra la paĝ' fantazia.
9 3 2 3 8
Kiel nebulo el tabulo mara,
4 6 2 6 4
Tra nia universo kaj ĉe lekcioj,
3 3 8 3 2 7
Cifervica poemo
9 5
Число π можно запомнить и с помощью мнемонической системы «Джордано», основанной на образном воспроизведении.
Изначально каждой цифре присваивают образ, состоящий из пары согласных букв. Например (этот вариант многие считают самым удачным):
0 – НМ, 1 – ГЖ, 2 – ДТ, 3 – КХ, 4 – ЧЩ, 5 – ПБ, 6 – ШЛ, 7 – СЗ, 8 – ВФ, 9 – РЦ.
Система кодирования простая: 6 - Шесть, 7 - Семь, 8 - Восемь. Отдельно стоят: Р - похожая на 9, Г - похожая на 1, и К - состоящая из 3х палочек. Вторые буквы созвучные первым. Кодирование одной цифры двумя буквами нужно для подбора слов для трехзначных чисел (получается 8 комбинаций букв при кодировании трехзначного числа).
Изображенный на фото ряд имеет другое объяснение, хотя и сходное.
- Машинописные t и d имеют только 1 идущий вниз штрих.
- Машинописная n имеет 2 идущих вниз штриха.
- Машинописная m имеет 3 идущих вниз штриха.
- Число 4 (four) заканчивается буквой r.
- Форма руки с четырьмя поднятыми вверх пальцами, когда большой палец повернут на 90 градусов, — это 5 пальцев в виде буквы L (прописной).
- Буква J (прописная) похожа на повернутую в обратную сторону 6.
- Букву К (прописную) можно нарисовать, сложив две семерки спиной к спине.
- Строчная буква f, написанная курсивом, выглядит как 8.
- Число 9 выглядит как повернутая в обратную сторону буква р или как перевернутая буква b.
- Слово zero (нуль) начинается с буквы z.
Аналогичные подсказки для русской кодировки:
- С буквы Р начинается слово «раз».
- С буквы Д начинается слово «два», а буква Г, набранная курсивом, напоминает цифру 2.
- С буквы Т начинается слово «три», а буква З похожа на цифру 3.
- С буквы Ч начинается слово «четыре», а с буквы К — слово «квадрат».
- С буквы П начинается слово «пять», а буква Б внешне и по звучанию похожа на цифру 5.
- С буквы Ш начинается слово «шесть», а буква Щ звучит похоже.
- С буквы С начинается слово «семь».
- С буквы В начинается слово «восемь», а буква Ф имеет сходное звучание.
- С буквы М начинается слово «много», так как 9 самая большая цифра.
- Буквы Н и Л в слове «НоЛь».
Давайте попробуем запомнить число π до двадцатого знака после запятой. Вот оно - 3,14159265358979323846…
Для этого сначала разобьем наши цифры на двузначные числа и запишем их в виде букв. Затем подберем слова, в которых будет по одной из букв каждой пары.
14 – ГЖ ЧЩ – ЖуЧок, 15 – ГЖ ПБ – ЖаБа, 92 – РЦ ДТ – РиТа, 65 – ШЛ ПБ – ЛиПа, 35 – КХ ПБ – КеПка, 89 – ВФ РЦ – ВеРно, 79 – СЗ РЦ – ЗаяЦ, 32 – КХ ДТ – КоТ, 38 – КХ ВФ – КоФе, 46 – ЧЩ ШЛ – ЧаШка.
Как видно, сначала идут 2 согласные, каждая их которых преобразуется в цифру, которую запоминаем.
У нас есть слова, которые нужно запомнить. Легче всего придумать из них рассказ.
"ЖуЧок и ЖаБа РиТа жили в лесу. Как-то раз под ЛиПой они нашли КеПку. ВеРно это ЗаяЦ или КоТ ее потеряли. Выпили друзья КоФе из ЧаШки и пошли искать кому принадлежит пропажа."
Остается запомнить рассказ и опорные слова. Затем перевести слова в цифры и удивить окружающих своей памятью.
Ученые нашли последнее число в разложении числа "π" - им оказалось число "е". А если серьезно, то неизвестно, являются ли числа π и e алгебраически независимыми, особенно если вспомнить тождество Эйлера.
 |
| тождество Эйлера на футболке Милхауса Ван Хутена (персонажа американского мультсериала «Симпсоны») |
e — число е, или основание натурального логарифма; Якоб Бернулли работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег, Ньютон же использовал эту модель, чтобы показать, как охлаждается чашка чая (это, может и не настолько популярно, как π, но у него тоже есть своя дата — 7 февраля);
i — мнимая единица, √(-1); Эйлер был также первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, Лейбниц дал такой комментарий о мнимом числе: "Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием"; (Уберите п из пи, и получится i! Конечно, это работает не так, но от этого i не перестаёт быть интересным. Как сделать i еще «страньше»? Например, возвести его в степень i. На первый взгляд может показаться, что это будем самым мнимым из всех мнимых чисел, но самом деле получается относительно нормальный результат: действительное число e-½π, что равняется примерно 0.207. И да, этот результат Эйлер получил еще в далеком 1746 году. Но, как отметил Эйлер, такой результат получается только при угле 90°. Вообще, у i в степени i бесконечно много результатов, просто так уж получилось, что один из этих результатов нормальный);
π — число пи, отношение длины окружности к длине её диаметра;
1 — единица, нейтральный элемент по операции умножения, основа любой системы исчисления; "Это единственно число, на которое все остальные делятся без остатка. Это единственное число, которое делится на единственное другое число — себя. Это единственное положительно целое число, которое не является ни простым, ни составным";
0 — ноль, нейтральный элемент по операции сложения, число для обозначения ничего;
принадлежащих к четырём классическим областям математики (числа 0 и 1 относятся к арифметике, i — к алгебре, π — к геометрии, а e — к математическому анализу), что мистически истолковывалось как символ единства математики. Кстати, связь экспоненты с тригонометрическими функциями не менее удивительна, ведь степенная функция стремится к бесконечности, а функции sin и cos колеблются в интервале от —1 до 1.
Формула Эйлера впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum), которая была издана в 1722 году, уже после смерти автора. Котс привёл её как небольшое предложение среди множества геометрических построений, которое после перевода на современный математический язык и исправления ошибки в знаке, имеет вид: ln(cos x+isin x)=ix. Эйлер опубликовал формулу в её привычном виде (та, что приведена на почтовой марке, выпущенная Швейцарией в 1957 г. в честь 250-й годовщины Эйлера) в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748), построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя у К.Весселя. Чтобы подчеркнуть красоту тождества Эйлера журнала Physics World в 2004 году задал своим читателям вопрос: "Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто?" Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике». Профессор математики Стэнфордского университета Кит Девлин в своем эссе «Самое прекрасное уравнение» (2002) сказал: «Как шекспировский сонет схватывает саму суть любви, или картина раскрывает красоту человеческой формы, намного более глубокую, чем просто кожа, уравнение Эйлера проникает в самые глубины существования». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу "…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой". По мнению же популяризатора математики Констанс Рид, это тождество является «самой знаменитой формулой во всей математике». Исследование мозга шестнадцати математиков показало, что «эмоциональный мозг» (в частности, медиальная орбитофронтальная кора, реагирующая на прекрасную музыку, поэзию, картины и т. д.) активировался более последовательно в случае тождества Эйлера, чем в отношении любой другой формулы. Тождеству Эйлера посвящён фильм японского кинорежиссёра и сценариста Такаси Коидзуми «Любимое уравнение профессора» (2006) с Акирой Тэрао в главной роли (номинация за лучшую мужскую роль премии Японской киноакадемии).
* Русский вариант до 15-го знака после запятой (e = 2,718281828459045...): Двум запятым семь вёрст не крюк (2,7) + два Льва Толстых (Год рождения Толстого 1828) + прямоугольный равнобедренный (углы равнобедренного прямоугольного треугольника - 45, 90, 45).
* Американский вариант связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — равнобедренный прямоугольный треугольник.
* Мнемоническое стихотворение, позволяющее запомнить первые 12 знаков после запятой (длины слов кодируют цифры числа e):
Мы порхали и блистали,
Но застряли в перевале:
Не признали наши крали
Авторалли.
* Французский вариант (цифры кодирует длина слов): "Tu aideras a rappeler ta quantite a beaucoup de docteurs amis".
* Английский вариант: "To express e, remember to memorize a sentence to simplify this".
* «Правило Боинга»: e ≈ 4 sin(0,747) даёт точность 0,0005.
* С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6−4, 6−2, 6−1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки):
а с точностью менее 0,001:
В 1996 году американский математик и писатель Майк Кейт издал мини-произведение «Ритмическая каденция» («Cadaeic Cadenza»), длина слов в тексте которого соответствовало почти четырем тысячам (3835) первых цифр числа π. Кстати, этот стиль написания с ограничениями, в котором длины последовательных слов соответствуют цифрам числа π, называется Pilish (пилиш). Первая часть названия этого произведения (Cadaeic) была также закодирована по специальной методике. В этой методике числа от 1 до 9 заменяются первыми девятью буквами выбранного алфавита, т.е. Cadaeic=3.141593. В русском языке для подобных целей можно использовать буквы от А до З включительно. Но насколько удобно будет запоминать составленные из них комбинации — решать вам.
Cовременный французский поэт-структуралист Жак Бене предлагает сочинять иррациональные сонеты, т.е. сонеты, у которых каноническое количество строк (14 строк) сохраняется, но со структурой, опирающейся на число π. Строки делятся по строфам в соответствии с десятичной записью числа π, при этом количество строк в сонете сохраняется: 3+1+4+1+5=14. Рифмы распредяляются следующим образом: ААb C bAAb C CdCCd (рефрен – четвертая строка). Поэт уже написал несколько стихотворений, удовлетворяющих такой схеме.
А вот этот стих, очень даже интересен:
Раз у Коли и Арины
Распороли мы перины.
Белый пух летал, кружился,
Куражился, замирал,
Ублажился,
Нам же дал
Головную боль старух.
Ух, опасен пуха дух!
— Георгий Александров
Американский математик и редактор журнала «Mathematics of Computation» Дэниел Шенкс, наиболее известный монографией «Решённые и нерешённые проблемы теории чисел», первым вычислил (в 1961 г., за 9 часов работы компьютера IBM 7090) более 100000 знаков числа π, значительно перекрыв достижение своего однофамильца британского математика-любителя Уильяма Шенкса, который в 1873 г., после двадцатилетних трудов, вычислил 707 знаков, и так гордился этим, что приказал выбить это число на своей могильной плите. Однако, в 1944 г. Д.Ф.Фергюсон (в сентябре 1949 г. вычисливший 1120 знаков числа π) с помощью механического настольного калькулятора обнаружил, что верных из них 527. (Уильям Шенкс также вычислил e и константу Эйлера-Маскерони γ с точностью до многих десятичных знаков. Он опубликовал таблицу простых чисел до 60 000 и нашел натуральные логарифмы 2, 3, 5 и 10 до 137 знаков.)
18 февраля 1995 года японский учёный Хирюки Гото (後藤 裕之) из Токио смог воспроизвести по памяти 42195 знаков числа π после запятой. В 2002 году он просчитал 1,24 триллиона цифр в числе π с помощью мощного компьютера Hitachi SR 8000. В октябре 2011 года число π было рассчитано с точностью до 10.000.000.000.000 знаков после запятой. Его рекорд побил китаец Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67890 знаков после запятой без ошибки. В том же 2006 году японец Акира Харагути заявил, что запомнил число π до 100-тысячного знака после запятой, однако проверить это официально не удалось.
17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор Андрей Слюсарчук установил мировой рекорд, запомнив 30 миллионов знаков числа π, которые были напечатаны в 20 томах текста. С установлением нового рекорда Андрея Слюсарчука официально поздравил Президент Украины Виктор Андреевич Ющенко. Поскольку устное перечисление 30 млн цифр π со скоростью одна цифра в секунду заняло бы почти год (347 дней) при непрерывном перечислении 24 часа в сутки, 7 дней в неделю, то был применён следующий подход для проверки рекорда: во время демонстраций г. Слюсарчука просят назвать произвольно выбранные проверяющими последовательности цифр числа π, расположенные на произвольно выбранных местах произвольных страниц 20-томной распечатки, группированной в упорядоченные таблицы. Он многократно успешно проходит этот тест. Свидетелями демонстраций были уважаемые учёные, доктора и кандидаты наук, заведующие кафедрами Институтов и Университетов. Книга рекордов Украины перечисляет членов комиссии, участвовавших в демонстрациях. Приведены их научные звания и занимаемые должности. Уникальная память Андрея Слюсарчука основана на эйдетическом восприятии информации.
Мдааа.. Я не потяну. А Вы?
Кстати, тем, кому трудно запомнить числа, но приходится работать с числом π, можно посоветовать сделать татуировку:
 |
| это тоже цифры, но дизайнерские. и тут 4 числа π |
 |
| Здесь точки представляют цифры числа π, начиная сверху и двигаясь по часовой стрелке |
 |
| похоже эта бесполезна, зато очень симпатична! |
Живёт по доброй воле
У Пи-числа в плену,
Когда же съест пуд соли -
Он снимет пелену!
Вы поглядите, ну:
Вот число по кличке Пи -
Подсчитай-ка, не сопи!
Это знали с древности...
Ты ж, забудь о лености.
Вспомни старый Вавилон -
Мудрецам большой поклон!
Рим, Египет и Китай,
Грекам древним дань отдай!
Антифон и с ним Бризон
Спели чуть не в унисон,
А за ними - Архимед.
Вот кто дали нам ответ!
Есть окружность, вот длина -
Подели давай-ка на:
На диаметр её же...
Не спеши-ка! Хм... Похоже!..
Три-Четырнадцать... Ура!
Ну, а дальше? Ох, дыра...
Сколько знаков без конца!..
Не послать ли нам гонца?
Нет. Ему их не догнать -
Жизнь так можно потерять...
Лучше, слышь, вина купи -
Тост подымем мы за Пи!
Serg Merisarov
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби, найденной Архимедом, является приближённым значением числа π. Впрочем, дробь 22/7 точнее приближается к числу π, чем 3.14 (если не учитывать и время: 1:59:26), так что 22 июля даже более подходящая дата для этого праздника. Кроме того, формат записи даты ДД/ММ или Д/М распространён гораздо шире, чем ММ/ДД, положенный в основу выбора даты 14 марта. Кроме того, «День приближённого числа Пи» также отмечается 10 ноября, так как это 314-й день года.
У π есть соперники. Существуют сторонники альтернативной константы τ (тау) = 2*π. По их мнению, отношение длины окружности к ее радиусу, а не диаметру, будет более естественным и позволит упростить формулы. Они предлагают отмечать «день Тау» (также известный как День двух Пи (двух Пирогов, если помните)) 28 июня, чтобы «съедать вдвое больше пи-рога». Впрочем, если серьезно, то бывший физик-теоретик, а ныне педагог Майкл Хартл из США считает, что вина числа π заключается всего лишь в том, что оно просто «неестественное»: "Данная буква означает именно то, что вы хотите - так называемое отношение длины окружности к диаметру. Однако посудите сами — ведь окружность не диаметром задается, а радиусом. В соответствии со стандартным определением, окружностью называется фигура, которая состоит из всех точек плоскости, отнесенных от некоего центра на конкретную длину — то есть на радиус. Когда же вы начинаете задавать геометрическую постоянную круга посредством отношения длины окружности к ее диаметру, то это можно считать ни чем иным, как делением ее на удвоенный радиус, и данная двойка станет преследовать ваш ум в процессе всех вычислений". По мнению ученого, использование числа τ (предложенного им в 2010 г.) избавит психику математика от этой самой «преследующей двойки» и сделает многие расчеты параметров окружности и круга проще, быстрее и удобнее. Физика Хартла поддерживает профессор Университета Юты (США) Роберт (Боб) Палэй, который еще в 2001 году опубликовал статью, в которой доказывал ошибочность применения числа π. А британец Кевин Хьюстон, математик из Университета Лидса, так защищает идею коллеги: "Удивительно, как люди раньше этого не поняли. Почти все, что мы делаем с числом Пи, мы можем делать и с числом Тау, но когда мы противопоставляем Пи и Тау, то Тау выигрывает - оно гораздо более натурально".
Есть люди, предлагающие использовать для этих целей новый знак (см. выше).
1592 г. — самый π-день в истории: 3.14.1592. Следующий такой день будет только в 15926 году. Есть пессимистическое подозрение, что мы не доживём. (из Абсурдопедии)
Леонардо да Винчи (1452-1519) и художник Альбрехт Дюрер (1471-1528) имели небольшие наработки по «квадратуре круга», то есть владели приблизительным значением числа Пи. Каббалистам, будет интересно, что частью гениальности изображения Леонардо является то, что в одном рисунке изображено одновременно 16 поз, а буква π — 16-я буква греческого алфавита (кстати, в английском алфавите буква p также занимает 16-ю позицию).
   |
| дворец Кастель дель Монте |
Впрочем, это не единственное сооружение на земном шаре, посвященное Пи.
Монумент Лудолфу ван Цейлену, или числу Пи, в Pieterskerk в Лейдене, созданный голландским типографом, членом Гильдии резчиков надписей Ирландии Марией Корнелией Элизабет Баккум.
Есть даже дорожка, которую оценят математики и сочувствующие.
Американская компания Decor Craft Inc. представила очередную разработку – оригинальные интерьерные часы для поклонников математики. Все значения на циферблате представлены в виде несложных математических задач. Так, например, 12 часов - это 6 x 2, 2 часа - это корень квадратный из 4, а 9 часов - это 3 x (π - 0.14).
Странные версии числа ПИ
5 февраля 1897 года, 111 лет назад, Генеральная Ассамблея штата Индиана чуть не утвердила билль 246 (по-нашему, законопроект), согласно которому число π принималось равным 3,2. Законопроект внес на рассмотрение республиканец Т.И.Рекорд, а автором идеи был непрофессиональный математик Эдвин Дж.Гудвин. Число π не упоминалось в нем напрямую, билль содержал только методику нахождения площади круга, предложенную Гудвином. Случайное присутствие в тот день на Ассамблее профессора-математика С.А.Уалдо из университета Пердью, который был там по другому вопросу, спасло истину. Вмешательство ученого помешало законодателям установить «новую математическую истину», утвердив безграмотный законопроект. Впрочем, законопроект не отклонили, а всего лишь отложили (на чёрный день, надо полагать). В отложенном состоянии он находится и до сих пор. Существует также версия о том, что в каком-то штате Америки принят закон, по которому число π равно 4, для того, чтобы было проще считать налоги на ввоз ковров, которые обычно в рулонах привозят, да и эти самые налоги были бы побольше. Однако это больше похоже на задорновщину, чем на реальный факт.
"Семьи за изучение правильных теорий" - группа активистов, созданная в американском штате Канзас для борьбы с влиянием религиозных традиционалистов на учебные программы школ. Ученые и преподаватели, объединившиеся в группу, пародируют требования так называемых креационистов. "На уроках математики надо объяснить школьникам, что число π равно трем, и без всяких десятичных знаков. Именно это следует из библейской Книги Царств, где описывается устройство бассейна для ритуальных омовений в храме, воздвигнутом Соломоном: "И сделал литое из меди море, - от края его до края его десять локтей, - совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом". Тогда получается, что число π равно только трём! Впрочем, академик РАО профессор Г.Глейзер, тщательно изучив хранящийся в Иерусалиме ивритский первоисточник Библии, обратил внимание на некоторую особенность в записи слова линия (“снурок”). В оригинале перед этим словом стоит одна лишняя буква, про которую на полях книги написано, что при чтении текста эта буква не должна произноситься. В традиционном еврейском учении каждой букве алфавита придается определённое числовое значение. Подсчитав сумму значений слова линия с учётом лишней буквы, профессор Глейзер получил более точное значение длины окружности - 31,415094. Разделив его на длину диаметра (10 локтей), получаем 3,1415094… с четырьмя верными десятичными знаками!
В мультсериала Симпсоны, в эпизоде "Bye Bye Nerdie" профессор Фринк громко кричит, что "π равно трем!" для того, чтобы привлечь внимание аудитории. Когда все поворачиваются, чтобы посмотреть на него, он извиняется за то, что был вынужден так святотатствовать.
В произведения Сергея Лукьяненко "Спектр" упоминаются миры, где π равно 4. Сразу вспоминается старый анекдот: "В военное время число Пи может достигать 4. Таким образом круг превращается в квадрат, а все дождевые капли - в куб, что в корне меняет их аэродинамику.(Электронный калькулятор специального (военного) применения. СССР. 1982 г.)" Вот Вам и "квадратура круга".
Профессор Эрнст
Вспоминается анекдот
Цитата из диплома: "Так как до этого места никто не дочитает, примем число π равным пяти. Иначе расчёты не сходятся, а искать ошибку мне лень."
А между тем, «число π для гренландских китов равно 3,14» написано в «Справочнике китобоя» 1960-х годов выпуска.
Впрочем, как сказал почетный член π-Клуба В. Шендерович: "На круглых дураков число «пи» не распространяется".
А вот ещё один математический розыгрыш от Театра Занимательной Науки.
Дано: окружность радиуса R. Кривая А (на рисунке красная) построена из двух полуокружностей радиуса R/2.
Следовательно, длина кривой А равна π×R.
Кривая B построена из четырёх полуокружностей радиуса R/4, её длина также равна π×R.
Аналогично, кривая C построена из восьми полуокружностей радиуса R/8 и длина её так же составляет Pi×R.
Продолжая построение, получим последовательность кривых, составленных из полуокружностей радиуса, стремящегося к нулю, длина всех этих кривых равна π×R.
Очевидно, что кривые, с увеличением числа составляющих полуокружностей и с уменьшением их радиуса, стремятся к отрезку MN, длина которого равна 2R.
Таким образом, в пределе получаем:
π×R = 2R, следовательно, π = 2!
А теперь – вопрос: доказано, что число π равно двум. Почему же повсеместно используется более длинное и неудобное значение 3,1415...?
Особого упоминания достойно восклицание "Пи здесь!", которое по легенде восходит к арабским математикам, которые искали новые цифры в числовом представлении числа π. В несколько искаженном виде это восклицание дожило и до наших дней. Можно так же добавить, что символ или численный аналог 3.14 используется в эвфемистическом замещении русского мата в письменной речи в интернет-общении, в частности в слогах слов, содержащих π. Например, понадобилось вам кого-то обвинить в нетрадиционной сексуальной ориентации на форуме, а браузер или какая-то контрольная программа не пропускает табуированную лексику. Тогда вы можете этому товарищу сообщить, что он - 3,1415, плюс первая нота в нотной гамме, плюс один. В смысле - "раз". С окончанием на "С".
Кстати, чёрную вязаную шапочку называют «пидорка». Знаете почему? Дело в том, что в расправленном виде вязаная шапочка имеет полусферическую форму. Чтобы получить длинну окружности, что будет являться размером головы, нужно число π (Пи) умножить на диаметр окружности Do. А чтобы узнать высоту полусферы, нужно учесть и радиус R. Только в таком случае мы будем иметь представление о размере шапочки. Полученную формулу дополним толщиной вязки k и диаметром шерстяной нити а. Выходит универсальная формула, характеризующая основные параметры шапочки Пи * Do * R * k * a. Следует учесть, что только в России название этой популярной шапочки имеет сугубо научные корни, что, разумеется, говорит о "высоком" культурном и образовательном уровне россиян.
 |
| Фото (Creative Commons license): ChrisDag |
А это где-то в KZ.
Комик Джон Эванс однажды язвительно заметил: «Что Вы получите, если разделите окружность фонаря из тыквы с прорезанными отверстиями в виде глаза, носа и рта на его диаметр? Тыкву π!».
Существует такая болезнь — графемно-цветовая синестезия — при которой индивидуальное восприятие графем (цифр и букв) ассоциируется с ощущением цвета. Однако, число π является в данном случае исключением, так как обладает собственным цветом: #314159. Шестнадцатеричный код цвета #314159 является средне-тмным оттенком сине-голубого. В модели цвета RGB #314159 составляет 19.22% красного, 25.49% зеленого и 34.9% синего. В цветовом пространстве HSL #314159 имеет оттенок 216° (градусов), 29% насыщенности и 27% светлости. Этот цвет имеет приблизительную длину волны в 476.45 nm.
и еще немного пи-юмора.
Пи-словарь
- π-анист - не менее, чем трижды рукоблуд
- π-астры — осенние цветы с количеством лепестков от 3 до 4
- π-жён — многоженец, у которого количество жен равно π
- π-кап — ускоренный счет капель лекарств тройками-четверками (например, при дозировке валокордина)
- π-капер - магистр Йода, снявший π тёлок
- π-люли - определенное количество люлей :-0)
- π-рог — волшебный зверь, приравниваемый к 3,14... единорогам
- π-рожное - более чем три рожи
- π-столет — юбилей известной константы
- π-стон — стон, три раза протяжный и один короткий
- π-тон — разновидность тритона
- у-π-танный — осведомлённый о π
 |
| представление цифр числа π в двоичной форме. |
 |
| Эта картина получена движением точки в зависимости от символа двоичного числа – 1 – поворот направо, 0 – налево |
 |
| Число π до стомиллиардного знака |
 |
| 4000000 цифр после запятой числа π. Дизайн-студия TWO-N. |
Можете и сами порисовать в стиле пи-арта:
Первые 2 картинки, думаю, пояснять не надо, просто рисуете точки в соответствии с выбранной цветовой гаммой чисел. А вот 3я требует некоего пояснения.
- Карандашом рисуете круг.
- На нем каждые 36 градусов ставите точку цветом в соответствии с выбранной цветовой гаммой чисел.
- Рисуете линию, соединяющую каждую цифру числа π со следующей, цвет линии должен соответствовать цвету точки старта этой линии.
- Продолжаете до тех пор, пока вам не надоест, или пока рисунок не начнет напоминать бабушкин клубок ниток, которым играл котенок.
Кстати, по этому же принципу Кристианом Иллесом Вэсилом нарисована и эта бесподобная картина. Художник всего лишь соединил разноцветными нитями последовательность первых 10 тыс. цифр числа π. Воплотить эту замечательную идею в жизнь ему позволила программа Circos, которая создает визуализации данных и информации в форме круга и используется в геномике. Идею Кристиана развил Мартин Кржывински. Он визуализировал вероятности перехода для первой тысячи значений числа π в один из десяти возможных сегментов. Тоже самое он проделал с первой тысячью значений чисел φ и e, а затем — с первыми двумя тысячами значений этих цифр. Далее Кржывински создал не менее прекрасную визуализацию числа π, разместив кружочки хорошо сочетающихся между собой оттенков красного, желтого и синего цветов на Архимедовой спирали. Получилось великолепно, судите сами:
Музыкант David Macdonald записал как звучит число π с точностью до 122 знаков после запятой.
Американская металкор группа из Миннеаполиса (штат Миннесота) "After the Burial", дебютный альбом "Forging" которой содержит композицию "A Future Self das Lied Pi" ("The Mercury God Of Infinity"), исполненную соло на акустической гитары, ритм которой основан на первых 110 цифрах числа π.
Кейт Буш посвятила числу π песню в опубликованном в 2005 году двойном альбоме "Aerial", в которой прозвучали 124 числа из знаменитого числового ряда 3,141… Впрочем, в песне неправильно названо 25-е число последовательности, да и потом исчезли куда-то целых 22 числа.
Число π связано и со спортом. В 2008 году в Южной Африке был придумана спортивная игра, основанная на числе π. Игра похожа на пляжный волейбол, но в нее играют в кругу, и вместо того, чтобы быть разделенными сеткой, игроки стоят напротив друг друга на площадке. Впрочем, эта игра была известна еще в СССР, и называлась "(горячая) картошка". Игроки становились в круг и перекидывали мяч друг другу в «волейбольной манере» не ловя его. Тот кто не смог отбить мяч (принять), садился в центр круга (в котёл). Сидя в «котле» он мог попытаться поймать пролетающий над головой мяч, но подниматься с корточек нельзя (если иное не оговорено правилами «картошка не растёт»). Если игроку удалось поймать мяч, будучи в «котле» он освобождал себя и других «пленных», а игрок, последний коснувшийся мяча перед этим занимал их место. Кроме того, игроки, перебрасывающие мяч, могли освободить кого-то из «котла». Для этого необходимо было попасть мячом в игрока, сидящего в центре круга, в случае промаха игрок присоединялся к сидящим. Игра продолжаелась до тех пор, пока не оставался только один игрок или пока она не надоедала участникам. Кроме того, игра под таким же названием, но с немного другими правилами, популярна и в англоязычных странах. Участники становятся в круг и под музыку стараются передать друг другу мяч (только не волейбольный, а небольшой теннисный маленький вязаный) как можно быстрее. Проигрывает тот, у кого мяч окажется в руках когда музыка закончится. Вместо музыки командовать процессом может и выбранный в этом случае ведущий, заканчивающий игру словами: «hot!», что на русский язык переводится как «горячо!». Происхождение игры точно неизвестно, возможно, она берёт своё начало в игре, описанной английским писателем Сидни Эдди в 1888 году. В собранном им словаре слов, употребляемых в Шеффилде, он описал правила игры, в чем-то схожей: участники становились в круг и передавали друг другу зажженную свечу. Каждый, у кого в руках оказывалась свеча, должен был произнести следующие слова: «Джек жив и любит жизнь, если он угаснет в твоих руках, ты должен будешь заплатить штраф». Тот, у кого свеча в руках гасла, расставался с обговорённой заранее суммой денег.
 |
| The Juice Is Loose («О Джей Симпсон на свободе») — 9 серия 7 сезона мультсериала «Гриффины», премьера 15 марта 2009 г. на канале FOX. |
Правда, здорово?
Уделите и вы немного своего драгоценного внимания числу π (Пи) в его хоть и неофициальный, но такой необычный праздник. Попытайтесь потренироваться в запоминании цифр после запятой или нарисовать число π или испеките Пи-пирог на радость себе и родным. А можно просто задуматься о тайнах, скрывающихся в бесконечном ряду цифр и над тем, что, вероятно, Космический Разум гораздо ближе к нам, чем мы полагаем…
www.calend.ru
ru.wikipedia.org
www.vokrugsveta.ru
arbuz.uz
www.chernov-trezin.narod.ru











































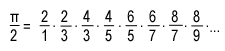
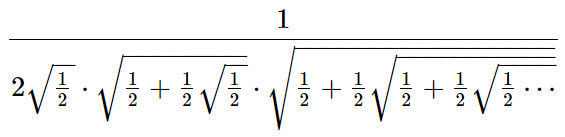






















































































оно не 3.14, а 3.375
ОтветитьУдалить1 апреля и не такие чудеса случаются)
УдалитьПи
ОтветитьУдалитьпи эр квадрат
Удалить